题目内容
8．若y=a|x|与y=x+a（a＞0）有两个公共点．则a的取值范围是（ ）| A． | （1．+∞） | B． | （0.1） | C． | ∅ | D． | （0.1）U（1，+∞） |
分析 画出图形，对a分类讨论，利用斜率与截距之间的关系即可得出．
解答 解：y=a|x|=$\left\{\begin{array}{l}{ax，x≥0}\\{-ax，x＜0}\end{array}\right.$，
当a=1时，两条直线平行；
当a＜1时，两条直线有且只有一个公共点；
当a＞1时，曲线y=a|x|与直线y=x+a（a＞0）有两个公共点．
故选A．
点评 本题考查了直线斜率与截距之间的关系、直线的交点、分类讨论方法，考查了数形结合的思想方法，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
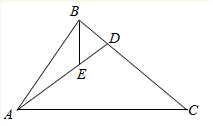如图，在△ABC中，已知∠BAC=$\frac{π}{3}$，|$\overrightarrow{AB}$|=2，|$\overrightarrow{AC}$|=3，点D为边BC上一点，满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$，点E是AD上一点，满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$，则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$．
16．已知集合A={x|（x-3）（x+1）≥0}，$B=\{y|y＜-\frac{4}{5}\}$，则A∩B=（ ）
| A． | {x|x≤-1} | B． | {x|x≥3} | C． | $\{x|x＜-\frac{5}{4}\}$ | D． | $\{x|-\frac{5}{4}≤x＜-1\}$ |
17．集合A={x|x≥0}，B={x|x2-1＜0}，则A∩B=（ ）
| A． | （-1，0] | B． | [0，1] | C． | （-1，1） | D． | [0，1） |
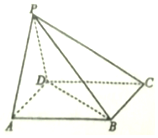如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD是正三角形，且平面PAD⊥平面ABCD．