Question

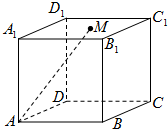
如图，ABCD-A₁B₁C₁D₁是正方体，在底面A₁B₁C₁D₁上任取一点M，则∠MAA₁≤

π

6

的概率P=（　　）

• A、

  π

  15

• B、

  π

  12

• C、

  π

  9

• D、

  π

  6

Answer 1

考点：几何概型

专题：计算题,概率与统计

分析：本题是几何概型问题，设棱长为3，∠MAA₁≤

π

6

表示以A₁为圆心，

3

为半径的

1

4

圆面，其面积为

3π

4

，求出正方形A₁B₁C₁D₁的面积为9，即可求出∠MAA₁≤

π

6

的概率

解答： 解：设棱长为3，则∠MAA₁=

π

6

时，MA₁=

3

，
∴∠MAA₁≤

π

6

表示以A₁为圆心，

3

为半径的

1

4

圆面，其面积为

3π

4

，
∵正方形A₁B₁C₁D₁的面积为9，
∴∠MAA₁≤

π

6

的概率P=

3π 4

9

=

π

12

．
故选：B．

点评：本小题主要考查几何概型、几何概型的应用、几何体和体积等基础知识，考查空间想象能力、化归与转化思想．属于基础题．