题目内容
过点 且被圆
且被圆 截得的弦长为8的直线方程为 .
截得的弦长为8的直线方程为 .
 且被圆
且被圆 截得的弦长为8的直线方程为 .
截得的弦长为8的直线方程为 . 和
和 ;
;解:圆心(0,0),r=5
圆心到弦的距离 的平方52-( )2 =9
)2 =9
若直线斜率不存在,则垂直x轴
x=3,圆心到直线距离=|0-3|=3,成立
若斜率存在
y-6=k(x-3)即:kx-y-3k+6=0
则圆心到直线距离|0-0-3k+6|
 =3
=3
解得k= 综上:x-3=0和3x-4y+15=0
综上:x-3=0和3x-4y+15=0
故答案为:x-3=0和3x-4y+15=0
圆心到弦的距离 的平方52-(
 )2 =9
)2 =9若直线斜率不存在,则垂直x轴
x=3,圆心到直线距离=|0-3|=3,成立
若斜率存在
y-6=k(x-3)即:kx-y-3k+6=0
则圆心到直线距离|0-0-3k+6|

 =3
=3解得k=
 综上:x-3=0和3x-4y+15=0
综上:x-3=0和3x-4y+15=0故答案为:x-3=0和3x-4y+15=0

练习册系列答案
相关题目
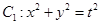 ,1<t<3,
,1<t<3,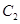 :
: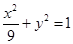 相交于A,B,C,D四点,点
相交于A,B,C,D四点,点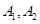 分别为
分别为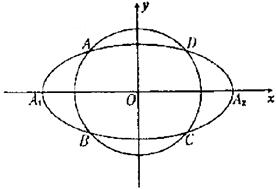
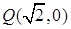 ,并且与定圆
,并且与定圆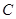 :
: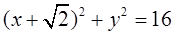 (圆心为C)相切.
(圆心为C)相切.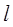 经过圆
经过圆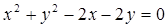 的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得
的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得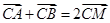 ?如果存在,求出
?如果存在,求出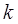 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由. 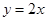 上一点
上一点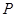 作圆
作圆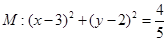 的两条切线
的两条切线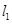 、
、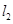 ,
,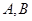 为切点,当
为切点,当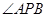 等于( )
等于( )



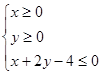 恰好被面积最小的圆C:
恰好被面积最小的圆C: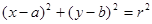 及其内部覆盖.
及其内部覆盖.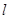 与圆C交于不同两点A、B,且
与圆C交于不同两点A、B,且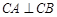 ,求直线
,求直线 过点A(3,1),且过点P(4,4)的直线PF与圆C相切并和x轴的负半轴相交于点F.
过点A(3,1),且过点P(4,4)的直线PF与圆C相切并和x轴的负半轴相交于点F. 的取值范围.
的取值范围.
 被圆
被圆 所截得的弦长为2,则
所截得的弦长为2,则 的值为 .
的值为 .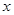 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为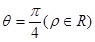 ,它与曲线
,它与曲线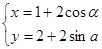 (
(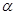 为参数)相交于两点A和B,则|AB|=______.
为参数)相交于两点A和B,则|AB|=______. 与圆
与圆 相切,且与直线
相切,且与直线
 平行,则直线
平行,则直线