题目内容
已知一动圆P(圆心为P)经过定点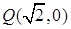 ,并且与定圆
,并且与定圆 :
: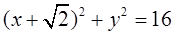 (圆心为C)相切.
(圆心为C)相切.
(1)求动圆圆心P的轨迹方程;
(2)若斜率为k的直线 经过圆
经过圆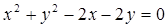 的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得
的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得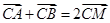 ?如果存在,求出
?如果存在,求出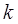 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
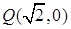 ,并且与定圆
,并且与定圆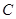 :
: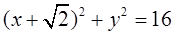 (圆心为C)相切.
(圆心为C)相切.(1)求动圆圆心P的轨迹方程;
(2)若斜率为k的直线
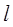 经过圆
经过圆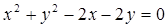 的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得
的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得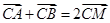 ?如果存在,求出
?如果存在,求出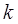 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由. (1)动圆圆心P的轨迹方程为 .
.
(2)存在常数 ,使得
,使得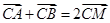 .
.
 .
. (2)存在常数
 ,使得
,使得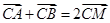 .
. (1)设P(x,y),动圆半径为r,则|PQ|=r.因为点Q在圆C的内部,所以动圆P与定圆C内切,所以|PC|=4-r.所以|PC|+|PQ|=4>|CQ|= ,由此能够求出动圆圆心P的轨迹方程.
,由此能够求出动圆圆心P的轨迹方程.
(2)假设存在常数k,使得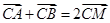 ,即
,即
 ,所以M为AB的中点.圆方程可化为
,所以M为AB的中点.圆方程可化为 ,所以由
,所以由 与
与 方程联立,消y后得到关于x的一元二次方程.因为点M(1,1)在椭圆的
方程联立,消y后得到关于x的一元二次方程.因为点M(1,1)在椭圆的 内部,所以恒有
内部,所以恒有 ,,由此能够推导出存在常数
,,由此能够推导出存在常数 ,使得
,使得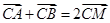 .
.
 ,由此能够求出动圆圆心P的轨迹方程.
,由此能够求出动圆圆心P的轨迹方程.(2)假设存在常数k,使得
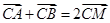 ,即
,即 ,所以M为AB的中点.圆方程可化为
,所以M为AB的中点.圆方程可化为 ,所以由
,所以由 与
与 方程联立,消y后得到关于x的一元二次方程.因为点M(1,1)在椭圆的
方程联立,消y后得到关于x的一元二次方程.因为点M(1,1)在椭圆的 内部,所以恒有
内部,所以恒有 ,,由此能够推导出存在常数
,,由此能够推导出存在常数 ,使得
,使得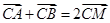 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
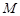 :
: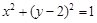 ,设点
,设点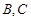 是直线
是直线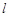 :
: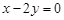 上的两点,它们的横坐标分别
上的两点,它们的横坐标分别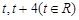 ,
,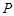 点的纵坐标为
点的纵坐标为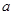 且点
且点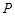 在线段
在线段 上,过
上,过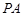 ,切点为
,切点为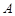
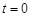 ,
,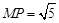 ,求直线
,求直线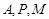 三点的圆的圆心是
三点的圆的圆心是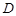 ,
,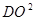 表示成
表示成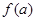 ,并写出定义域.
,并写出定义域.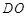 长的最小值
长的最小值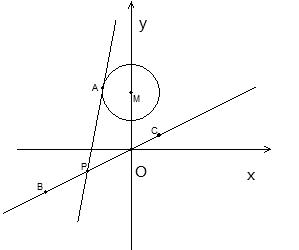
 中,以坐标原点
中,以坐标原点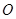 为圆心的圆与直线:
为圆心的圆与直线: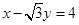 相切.
相切.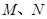 关于直线
关于直线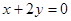 对称,且
对称,且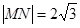 ,求直线MN的方程.
,求直线MN的方程. 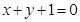 被圆
被圆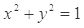 所截得的弦长为 ( )
所截得的弦长为 ( ) 


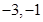 )两点,且两圆圆心都在直线
)两点,且两圆圆心都在直线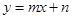 上,则
上,则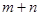 = .
= .

 且被圆
且被圆 截得的弦长为8的直线方程为 .
截得的弦长为8的直线方程为 . 过圆
过圆 的圆心,则
的圆心,则 的值为 ( )
的值为 ( ) 1
1