题目内容
设s>1,t>1,m∈R,x=logst+logts,y=logs4t+logt4s+m(logs2t+logt2s).
(1)将y表示成x的函数f(x),并求定义域;
(2)若关于x的方程f(x)=0有唯一实数解,求实数m的取值范围.
(1)将y表示成x的函数f(x),并求定义域;
(2)若关于x的方程f(x)=0有唯一实数解,求实数m的取值范围.
考点:函数解析式的求解及常用方法,对数的运算性质,根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)利用基本不等式求出f(x)的定义域,先求x2的表达式,再求y的表达式即可;
(2)利用分离常数法,求出m的表达式,根据函数的单调性,求出m的取值范围.
(2)利用分离常数法,求出m的表达式,根据函数的单调性,求出m的取值范围.
解答:
解:(1)∵s>1,t>1,∴logst>0,logts>0,
∴x=logst+logts≥2;
x2=log2st+log2ts+2,
∴log2st+log2ts=x2-2,
∴logs4t+logt4s=(x2-2)2-2;
∴y=(x2-2)2-2+m(x2-2)=(x2-2)2+m(x2-2)-2,定义域是[2,+∞);
(2)根据题意,方程(x2-2)2+m(x2-2)-2=0在[2,+∞)上有唯一实数解,
即m=-(x2-2)+
;
设m=g(x)=-(x2-2)+
(x≥2),
令u=x2-2,其中x∈[2,+∞),
则m是u的减函数;
即m=g(x)是定义域∈[2,+∞)上的减函数,
∴m≤g(2)=-1,即实数m的取值范围是m∈(-∞,-1).
∴x=logst+logts≥2;
x2=log2st+log2ts+2,
∴log2st+log2ts=x2-2,
∴logs4t+logt4s=(x2-2)2-2;
∴y=(x2-2)2-2+m(x2-2)=(x2-2)2+m(x2-2)-2,定义域是[2,+∞);
(2)根据题意,方程(x2-2)2+m(x2-2)-2=0在[2,+∞)上有唯一实数解,
即m=-(x2-2)+
| 2 |
| x2-2 |
设m=g(x)=-(x2-2)+
| 1 |
| x2-2 |
令u=x2-2,其中x∈[2,+∞),
则m是u的减函数;
即m=g(x)是定义域∈[2,+∞)上的减函数,
∴m≤g(2)=-1,即实数m的取值范围是m∈(-∞,-1).
点评:本题考查了求函数定义域的应用问题,也考查了函数的单调性问题,基本不等式的应用问题,是综合性题目.

练习册系列答案
相关题目
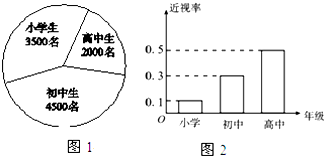
已知某地区中小学生人数和近视情况分别如图1和图2所示.为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )

| A、200,20 |
| B、100,20 |
| C、200,10 |
| D、100,10 |