Question

13．在棱长为a的正方体ABCD-A₁B₁C₁D₁中，点M是AB的中点，则点A到平面A₁DM的距离为（　　）

• A． $\frac{\sqrt{6}}{6}$a
• B． $\frac{\sqrt{6}}{3}$a
• C． $\frac{\sqrt{2}}{2}$a
• D． $\frac{1}{2}$a

Answer 1

分析 利用三棱锥的体积公式进行转换，即可求出点A到平面A₁DM的距离．

解答 解：棱长为a的正方体ABCD-A₁B₁C₁D₁中，点M是AB的中点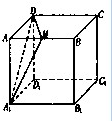，则AM=$\frac{1}{2}a$，A₁B=$\sqrt{2}a$，A₁M=$\frac{\sqrt{5}}{2}a$，
BM=$\frac{\sqrt{5}}{2}a$，
设点A到平面A₁DM的距离为：h；
则${V}_{A-{A}_{1}BM}={V}_{{A}_{1}-ABM}$，
可得$\frac{1}{3}$${S}_{△{A}_{1}BM}$•h=$\frac{1}{3}$S_△ABM•AA₁，
可得$\frac{1}{2}$×$\sqrt{2}×\sqrt{（\frac{\sqrt{5}}{2}）^{2}-（\frac{\sqrt{2}}{2}）^{2}}$a²h=$\frac{1}{2}×a×\frac{1}{2}a×a$，
解得h=$\frac{\sqrt{6}}{6}a$．
故选：A．

点评 本题以正方体为载体，考查了立体几何中点、线、面的距离的计算，属于中档题．运用体积计算公式，进行等体积转换来求点到平面的距离，是解决本题的关键．