题目内容
已知直线ax+y-1=0与直线x+ay-1=0互相垂直，则a=（ ）
| A、1或-1 | B、1 | C、-1 | D、0 |
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：直接由两直线垂直得到两直线系数间的关系，然后求解关于a的方程得答案．
解答：
解：∵直线ax+y-1=0与直线x+ay-1=0互相垂直，
∴1×a+1×a=0，即2a=0，解得：a=0．
故选：D．
∴1×a+1×a=0，即2a=0，解得：a=0．
故选：D．
点评：本题考查了直线的一般式方程与直线垂直的关系，关键是对条件的记忆与运用，是基础题．
练习册系列答案
相关题目
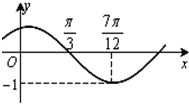函数f（x）=sin（ωx+φ）（其中|φ|＜| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
如图，已知△ABC中，D为BC的中点，E，F为BC的三等分点，若以原点O为中心，焦点在x轴上的双曲线C，有一条渐近线的倾斜角为60°，点F是该双曲线的右焦点．位于第一象限内的点M在双曲线C上，且点N是线段MF的中点．若|
|=|
|+1，则双曲线C的方程为（ ）
| ON |
| NF |
A、x2-
| ||||
B、x2-
| ||||
C、
| ||||
| D、3x2-y2=1 |
已知集合A={x|0＜x＜5}，B={x|x2-2x-3＞0}，则A∩∁RB（ ）
| A、（0，3） |
| B、（3，5） |
| C、（-1，0） |
| D、（0，3] |