题目内容
已知命题p:
<1,命题q:
≤1,则p是q的( )
| x+1 |
| 2x |
| x-1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:先解出命题p,q下的不等式,得到:p:-1≤x<0,q:-1≤x<1,这样即可判断p,q的关系.
解答:
解:命题p:解
<1得-1≤x<0;
命题q:解
≤1得-1≤x<1;
∴若p成立,则q一定成立,即p是q的充分条件;
若q成立,则p不一定成立,即p不是q的必要条件;
∴p是q的充分不必要条件.
故选:A.
| x+1 |
命题q:解
| 2x |
| x-1 |
∴若p成立,则q一定成立,即p是q的充分条件;
若q成立,则p不一定成立,即p不是q的必要条件;
∴p是q的充分不必要条件.
故选:A.
点评:考查无理不等式,分式不等式的解法,充分条件、必要条件、充分不必要条件的概念.

练习册系列答案
相关题目
下列命题正确的个数是①
+
=
②
•
=
③
-
=
④0•
=0( )
| AB |
| BA |
| 0 |
| 0 |
| AB |
| 0 |
| AB |
| AC |
| BC |
| AB |
| A、1 | B、2 | C、3 | D、4 |
数列{an}的前n项和Sn与通项公式an满足关系式Sn=nan+2n2-2n(n∈N*),则a100-a10=( )
| A、-90 | B、-180 |
| C、-360 | D、-400 |
半径为3cm,中心角为
的弧长为( )
| 2π |
| 3 |
A、
| ||
| B、πcm | ||
C、
| ||
| D、2πcm |
△ABC的面积是S,点P是△ABC的边AB上的一点,则△PBC的面积小于
的概率是( )
| S |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1(a>0,b>0)的渐近线经过点(2,1),则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
| ∫ |
-
|
| A、0 | ||
| B、2 | ||
C、
| ||
D、
|
复数(1-2i)2的虚部为( )
| A、-4 | B、-2 | C、2 | D、2i |
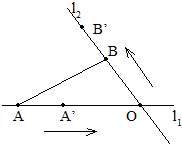 为进行科学实验,观测小球A、B在两条相交成60°角的直线型轨道上运动的情况,如图所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道l1、l2按箭头的方向运动.问:
为进行科学实验,观测小球A、B在两条相交成60°角的直线型轨道上运动的情况,如图所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道l1、l2按箭头的方向运动.问: