题目内容
已知△ABC中，AD、BE分别为BC、AC边的中线且AD⊥BE，则cosC的最小值为 ．
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：先设AC=2a，BC=2b，求出CE=a，CD=b，利用向量的减法得
=
-
、
=
-
，根据AD⊥BE得
•
=0，利用数量积的定义和运算律化简后，再根据基本不等式求出cosC的最小值．
| AD |
| CD |
| CA |
| BE |
| CE |
| CB |
| AD |
| BE |
解答：
解：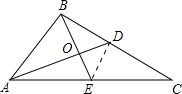
设AC=2a，BC=2b，则CE=a，CD=b，
因为
=
-
，
=
-
，且AD⊥BE，
所以
•
=(
-
)•(
-
)=0，
•
-
•
-
•
+
•
=0，
abcosC-2a2cos0°-2b2cos0°+4abcosC=0，
即cosC=
≥
=
（当且仅当a=b时取等号），
所以cosC的最小值为：
，
故答案为：
．
设AC=2a，BC=2b，则CE=a，CD=b，因为
| AD |
| CD |
| CA |
| BE |
| CE |
| CB |
所以
| AD |
| BE |
| CE |
| CB |
| CD |
| CA |
| CE |
| CD |
| CE |
| CA |
| CB |
| CD |
| CB |
| CA |
abcosC-2a2cos0°-2b2cos0°+4abcosC=0，
即cosC=
| 2(a2+b2) |
| 5ab |
| 2×2ab |
| 5ab |
| 4 |
| 5 |
所以cosC的最小值为：
| 4 |
| 5 |
故答案为：
| 4 |
| 5 |
点评：本题考查了向量的减法运算，向量垂直的条件，数量积的定义和运算律，基本不等式求最值问题，把角的余弦值问题转化为数量积运算要简单些．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知集合A={y|y=log2x，x＞1}，集合B={y|y=（
）x}，x＜1}，则A∩B=（ ）
| 1 |
| 2 |
A、{y|y＞
| ||
B、{y|{0＜y＜
| ||
| C、{y|y＞1} | ||
D、{y|
|