题目内容
11.已知x,y>0,且x+y=1,则$\frac{1}{2x+1}$+$\frac{4}{2y+1}$的最小值为$\frac{9}{4}$.分析 易知2x+1+2y+1=4,从而化简$\frac{1}{2x+1}$+$\frac{4}{2y+1}$=$\frac{1}{4}$•$\frac{2y+1}{2x+1}$+$\frac{2x+1}{2y+1}$+$\frac{5}{4}$,从而利用基本不等式求解.
解答 解:∵x+y=1,
∴2x+1+2y+1=4,
∴$\frac{1}{2x+1}$+$\frac{4}{2y+1}$
=$\frac{1}{4}$•$\frac{2x+1+2y+1}{2x+1}$+$\frac{2x+1+2y+1}{2y+1}$
=$\frac{1}{4}$•$\frac{2y+1}{2x+1}$+$\frac{2x+1}{2y+1}$+$\frac{5}{4}$
≥2$\sqrt{\frac{1}{4}}$+$\frac{5}{4}$=$\frac{9}{4}$,
(当且仅当$\frac{1}{4}$•$\frac{2y+1}{2x+1}$=$\frac{2x+1}{2y+1}$,即x=$\frac{1}{6}$,y=$\frac{5}{6}$时,等号成立),
故答案为:$\frac{9}{4}$.
点评 本题考查了基本不等式的变形应用及学生的化简运算能力的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.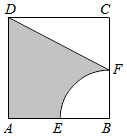 如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
 如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )| A. | π | B. | 6π | C. | $\frac{4π}{3}$ | D. | 4π |
3.用1,2,3,4四个数字组成一个四位数,其中大于3300的偶数有多少个( )
| A. | 128 | B. | 64 | C. | 96 | D. | 48 |