题目内容
6.在极坐标系中,已知点$A(2,\frac{π}{4})$,圆C的方程为$ρ=4\sqrt{2}sinθ$(圆心为点C),求直线AC的极坐标方程.分析 先求出直线AC的直角坐标方程,再转化为极坐标方程.
解答 解:点A的直角坐标为A($\sqrt{2}$,$\sqrt{2}$).
圆C的普通方程为x2+y2-4$\sqrt{2}$y=0,即x2+(y-2$\sqrt{2}$)2=8.
∴圆C的圆心为C(0,2$\sqrt{2}$).
∴直线AC的方程为$\frac{y-\sqrt{2}}{\sqrt{2}}=\frac{x-\sqrt{2}}{-\sqrt{2}}$,即x+y-2$\sqrt{2}$=0.
∴直线AC的极坐标方程为ρcosθ+ρsinθ-2$\sqrt{2}=0$.
点评 本题考查了极坐标方程与直角坐标方程的转化,属于基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
11.二项式${(9x-\frac{1}{{3\root{3}{x}}})^9}$的展开式中x的系数等于( )
| A. | 84 | B. | 24 | C. | 6 | D. | -24 |
18.已知实数x,y满足条件$\left\{\begin{array}{l}x-y≥-1\\ x+y≤4\\ x-2y≤0\end{array}\right.$,若使z=ax+y取到最大值的最优解有无数个,则实数a=( )
| A. | -1 | B. | 1 | C. | ±1 | D. | $-\frac{1}{2}$ |
16.若方程x2-1995x-1996=0和x2+1995x-1996=0的较小根分别为a和b,则ab的值为( )
| A. | 1 | B. | -1 | C. | 1996 | D. | -1996 |
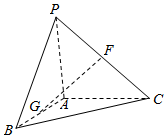 如图,在三棱锥P-ABC中,F、G、H分别是PC、AB、BC的中点,PA⊥平面ABC,PA=AB=AC=2,二面角B-PA-C为120°.
如图,在三棱锥P-ABC中,F、G、H分别是PC、AB、BC的中点,PA⊥平面ABC,PA=AB=AC=2,二面角B-PA-C为120°.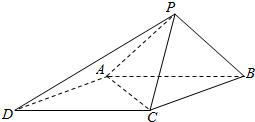 如图,已知在四陵锥P-ABCD中,底面ABCD是边长为2的菱形,∠BCD=120°,AP=BP,∠APB=90°,PC=2.
如图,已知在四陵锥P-ABCD中,底面ABCD是边长为2的菱形,∠BCD=120°,AP=BP,∠APB=90°,PC=2.