题目内容
f(x)=axekx-1,g(x)=lnx+kx.
(Ⅰ)当a=1时,若f(x)在(1,+∞)上为减函数,g(x)在(0,1)上是增函数,求k值;
(Ⅱ)对于任意k>0,x>0,f(x)>g(x)恒成立,求a的取值范围.
(Ⅰ)当a=1时,若f(x)在(1,+∞)上为减函数,g(x)在(0,1)上是增函数,求k值;
(Ⅱ)对于任意k>0,x>0,f(x)>g(x)恒成立,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)a=1时,f(x)=xekx-1,分别求出函数f(x),g(x)的导数,从而得出k的取值范围;
(Ⅱ)设h(x)=f(x)-g(x)=axekx-lnx-kx-1(x>0),求出h(x)的导数,通过讨论a的取值范围解决问题.
(Ⅱ)设h(x)=f(x)-g(x)=axekx-lnx-kx-1(x>0),求出h(x)的导数,通过讨论a的取值范围解决问题.
解答:
解:(Ⅰ)a=1时,f(x)=xekx-1,
∴f′(x)=(kx+1)ekx,g′(x)=
+k,
f(x)在(1,+∞)上为减函数,
则?x>1,f′(x)≤0?k≤-
,
∴k≤-1;
∵g(x)在(0,1)上为增函数,
则?x∈(0,1),g′(x)≥0?k≥-
,
∴k≥-1;
综上所述:k=-1.
(Ⅱ)设h(x)=f(x)-g(x)=axekx-lnx-kx-1(x>0),
∴h′(x)=(kx+1)(aekx-
),
设u(x)=aekx-
,
∴u′(x)=akekx+
,
①a≤0时,u(x)=aekx-
<0,
则h′(x)=(kx+1)(aekx-
)<0,
∴h(x)在(0,+∞)上是减函数,
h(x)>0不恒成立;
②当a>0时,u′(x)=akekx+
>0,
则在(0,+∞)上,u(x)=aekx-
是增函数,
u(x)的函数值由负到正,必有x0∈(0,+∞),u(x0)=0,
即aekx0=
,两边取自然对数得,lna+kx0=-lnx0,
h(x)在(0,x0)上是减函数,(x0,+∞)上是增函数,
h(x)min=h(x0)=ax0ekx0-1-lnx0-kx0
=1-1-lnx0-kx0
=-lnx0-kx0
=lna
因此,lna>0,
即a的取值范围是(1,+∞).
∴f′(x)=(kx+1)ekx,g′(x)=
| 1 |
| x |
f(x)在(1,+∞)上为减函数,
则?x>1,f′(x)≤0?k≤-
| 1 |
| x |
∴k≤-1;
∵g(x)在(0,1)上为增函数,
则?x∈(0,1),g′(x)≥0?k≥-
| 1 |
| x |
∴k≥-1;
综上所述:k=-1.
(Ⅱ)设h(x)=f(x)-g(x)=axekx-lnx-kx-1(x>0),
∴h′(x)=(kx+1)(aekx-
| 1 |
| x |
设u(x)=aekx-
| 1 |
| x |
∴u′(x)=akekx+
| 1 |
| x2 |
①a≤0时,u(x)=aekx-
| 1 |
| x |
则h′(x)=(kx+1)(aekx-
| 1 |
| x |
∴h(x)在(0,+∞)上是减函数,
h(x)>0不恒成立;
②当a>0时,u′(x)=akekx+
| 1 |
| x2 |
则在(0,+∞)上,u(x)=aekx-
| 1 |
| x |
u(x)的函数值由负到正,必有x0∈(0,+∞),u(x0)=0,
即aekx0=
| 1 |
| x0 |
h(x)在(0,x0)上是减函数,(x0,+∞)上是增函数,
h(x)min=h(x0)=ax0ekx0-1-lnx0-kx0
=1-1-lnx0-kx0
=-lnx0-kx0
=lna
因此,lna>0,
即a的取值范围是(1,+∞).
点评:本题考察了函数的单调性,导数的应用,求参数的取值,本题是一道综合题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
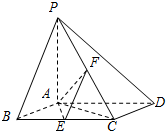 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.