题目内容
设项数均为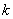 (
( )的数列
)的数列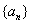 、
、 、
、 前
前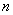 项的和分别为
项的和分别为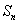 、
、 、
、 . 已知集合
. 已知集合 =
= .
.
(1)已知 ,求数列
,求数列 的通项公式;
的通项公式;
(2)若
 ,试研究
,试研究 和
和 时是否存在符合条件的数列对(
时是否存在符合条件的数列对(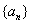 ,
, ),并说明理由;
),并说明理由;
(3)若 ,对于固定的
,对于固定的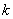 ,求证:符合条件的数列对(
,求证:符合条件的数列对(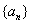 ,
, )有偶数对.
)有偶数对.
(1) ;(2)
;(2) 时,数列
时,数列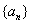 、
、 可以为(不唯一)6,12,16,14;2,8,10,4,
可以为(不唯一)6,12,16,14;2,8,10,4, 时,数列对(
时,数列对(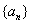 ,
, )不存在.(3)证明见解析.
)不存在.(3)证明见解析.
 6,12,16,14;2,8,10,4 ② 16, 10,8,14;12,6,2,4 …………………8分
6,12,16,14;2,8,10,4 ② 16, 10,8,14;12,6,2,4 …………………8分
当 时,
时,



此时 不存在. 故数列对(
不存在. 故数列对(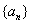 ,
, )不存在. ………………………………10分
)不存在. ………………………………10分
另证:
当 时,
时,



练习册系列答案
相关题目
 及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为
及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为 B.
B.  C.
C.  D.
D. 

 的圆心到直线
的圆心到直线
 (
( )的距离为
)的距离为 ,则
,则 .
. 的前
的前 ,若
,若 (
( .
.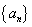 的前
的前 ,其中
,其中 、
、 、
、 是常数.
是常数. ,
, ,
, ,求数列
,求数列 ,
, ,
, ,且
,且 ,求数列
,求数列 的等比数列.
的等比数列. 满足
满足 ,则目标函数
,则目标函数 -1的最大值为
-1的最大值为 D.
D. 
 的边长是3,
的边长是3, 是
是 上的点,BD=1,则
上的点,BD=1,则 =
= B.
B. C.
C. D.
D.
 的倾斜角是
的倾斜角是 ,则
,则 (结果用反三角函数值表示).
(结果用反三角函数值表示). 展开式中含
展开式中含 项的系数是_________.
项的系数是_________.