题目内容
17.复数$\frac{2}{i(3-i)}$=( )| A. | $\frac{1-3i}{5}$ | B. | $\frac{1+3i}{5}$ | C. | $\frac{3+i}{5}$ | D. | $\frac{3-i}{5}$ |
分析 直接利用复数代数形式的乘除运算化简得答案.
解答 解:$\frac{2}{i(3-i)}$=$\frac{2}{3i-{i}^{2}}=\frac{2}{1+3i}=\frac{2(1-3i)}{(1+3i)(1-3i)}=\frac{2-6i}{10}$=$\frac{1-3i}{5}$.
故选:A.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
相关题目
8.设数列{an}为等差数列,Sn为其前n项和,若S1≤13,S4≥10,S5≤15,则a4的最大值为( )
| A. | 3 | B. | 4 | C. | -7 | D. | -5 |
9.命题“?n∈N,f(n)∉N且f(n)≤n”的否定形式是( )
| A. | ?n∈N,f(n)∈N且f(n)>n | B. | ?n0∈N,f(n0)∈N且f(n0)>n0 | ||
| C. | ?n∈N,f(n)∈N或f(n)>n | D. | ?n0∈N,f(n0)∈N或f(n0)>n0 |
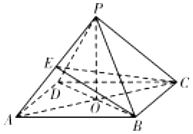 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=3,PA=$\sqrt{11}$,AC∩BD=O.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=3,PA=$\sqrt{11}$,AC∩BD=O.