题目内容
13. 已知点F为抛物线E:y2=2px(p>0)的焦点,点A(3,m)在抛物线E上,且|AF|=4.
已知点F为抛物线E:y2=2px(p>0)的焦点,点A(3,m)在抛物线E上,且|AF|=4.(Ⅰ)求抛物线E的方程;
(Ⅱ)已知点G(-1,0),延长AF交抛物线E于点B,证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
分析 (I)由抛物线定义可得:|AF|=3+$\frac{p}{2}$=4,解得p.即可得出抛物线E的方程.
(II)由点A(3,m)在抛物线E上,解得m,不妨取A(3,2$\sqrt{3}$),F(1,0),可得直线AF的方程,与抛物线方程联立化为3x2-10x+3=0,解得B($\frac{1}{3}$,-$\frac{2\sqrt{3}}{3}$).又G(-1,0),计算kGA,kGB,可得kGA+kGB=0,∠AGF=∠BGF,即可证明以点F为圆心且与直线GA相切的圆,必与直线GB相切.
解答 (I)解:由抛物线定义可得:|AF|=3+$\frac{p}{2}$=4,解得p=2.
∴抛物线E的方程为y2=4x;
(II)证明:∵点A(3,m)在抛物线E上,
∴m2=4×3,解得m=±2$\sqrt{3}$,不妨取A(3,2$\sqrt{3}$),F(1,0),
∴直线AF的方程:y=$\sqrt{3}$(x-1),
联立抛物线,化为3x2-10x+3=0,解得x=3或$\frac{1}{3}$,B($\frac{1}{3}$,-$\frac{2\sqrt{3}}{3}$).
又G(-1,0),∴kGA=$\frac{\sqrt{3}}{2}$.kGB=-$\frac{\sqrt{3}}{2}$,
∴kGA+kGB=0,
∴∠AGF=∠BGF,∴x轴平分∠AGB,
因此点F到直线GA,GB的距离相等,
∴以点F为圆心且与直线GA相切的圆,必与直线GB相切.
点评 本小题主要考查抛物线、直线与抛物线及其圆的位置关系及其性质、点到直线的距离公式等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想,属于难题.

练习册系列答案
相关题目
3.下列结论①(sinx)′=-cosx;②$(\frac{1}{x})'=\frac{1}{x^2}$;③$({log_3}x)'=\frac{1}{3lnx}$;④$({x^2})'=\frac{1}{x}$.其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
4.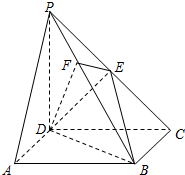 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(Ⅰ)求证:DE⊥平面PBC;
(Ⅱ)求二面角F-DE-B的正弦值.
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.(Ⅰ)求证:DE⊥平面PBC;
(Ⅱ)求二面角F-DE-B的正弦值.
8.已知函数f(x)=ax3+x+1的图象在点(1,f(1))的处的切线过点(2,11),则 a=( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{4}$ | C. | 1 | D. | 2 |
 (1)计算:${27^{\frac{2}{3}}}-{2^{{{log}_2}3}}×{log_2}\frac{1}{8}+2lg({\sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}})$
(1)计算:${27^{\frac{2}{3}}}-{2^{{{log}_2}3}}×{log_2}\frac{1}{8}+2lg({\sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}})$