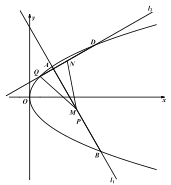
题目内容
【题目】已知椭圆
的离心率为
，左、右焦点分别为
，
，
为椭圆C上一点.
（1）求椭圆C的方程；
（2）设椭圆C的左、右顶点分别为
，
，过，分别作x轴的垂线
，
，椭圆C的一条切线
与，交于M，N两点，求证：
是定值.
【答案】（1）
；（2）证明见解析.
【解析】
(1)根据椭圆离心率，将点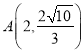
代入椭圆方程，由此即可求出椭圆方程；
(2)由题设知
，
与
的方程联立消去
可得
，再根据判别式可得
，再求出点
的坐标，根据向量的数量积即可证明．
(1)由题意可知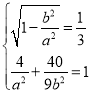
得
，
故所求椭圆C的标准方程为；
(2)证明：由题意可知，
的方程为
，
的方程为
，
直线l与直线，联立可得
，
，
所以
，
.
所以
.
联立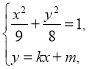
得
因为直线l与椭圆C相切，
所以
，
化简，得.
所以，
所以
，故
为定值
(注：可以先通过
计算出此时
，再验证一般性)
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务，由于其依托“互联网+”，符合“低碳出行”的理念，已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管，随机选取了50人就该城市共享单车的推行情况进行问卷调査，并将问卷中的这50人根据其满意度评分值（百分制）按照
分成5组，请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图（如图所示）解决下列问题：
频率分布表
组别 | 分组 | 频数 | 频率 |
第1组 |
| 8 | 0.16 |
第2组 |
|
| ▆ |
第3组 |
| 20 | 0.40 |
第4组 |
| ▆ | 0.08 |
第5组 |
| 2 |
|
合计 | ▆ | ▆ |
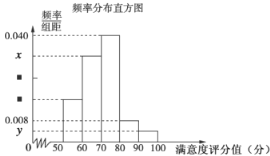
（1）求
的值；
（2）若在满意度评分值为
的人中随机抽取2人进行座谈，求所抽取的2人中至少一人来自第5组的概率.
