题目内容
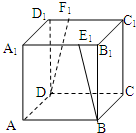ABCD-A1B1C1D1是正方体，B1E1=D1F1=| A1B1 | 4 |
分析：取A1M=B1F1，再取AB的中点N，由正方体的性质可得∠BE1N为BE1与DF1所成的角，△BE1N中，由余弦定理
求得cos∠BE1N=
，从而得到∠BE1N=arccos
．
求得cos∠BE1N=
| 15 |
| 17 |
| 15 |
| 17 |
解答：解：如图所示：取A1M=B1F1，则由正方体的性质可得A1M 与 B1F1 平行且相等．
再取AB的中点N，则由ME1∥AN 且 ME1=AN，可得ME1AN 为平行四边形，AM∥NE1，且AM=NE1．
∠BE1N为BE1与DF1所成的角．
设正方体的冷场为1，△BE1N中，NB=
，NE1=
=
=BE1．
由余弦定理可得
=
+
-2
×
cos∠BE1N，
解得cos∠BE1N=
，∴∠BE1N=arccos
．
故答案为：arccos
．
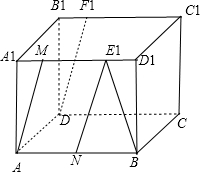
再取AB的中点N，则由ME1∥AN 且 ME1=AN，可得ME1AN 为平行四边形，AM∥NE1，且AM=NE1．
∠BE1N为BE1与DF1所成的角．
设正方体的冷场为1，△BE1N中，NB=
| 1 |
| 2 |
1+(
|
| ||
| 4 |
由余弦定理可得
| 1 |
| 4 |
| 17 |
| 16 |
| 17 |
| 16 |
| ||
| 4 |
| ||
| 4 |
解得cos∠BE1N=
| 15 |
| 17 |
| 15 |
| 17 |
故答案为：arccos
| 15 |
| 17 |
点评：本题主要考查直线和平面所成的角的定义和求法，体现了数形结合的数学思想，找出直线和平面所成的角，
是解题的关键．
是解题的关键．
练习册系列答案
相关题目
已知长方体ABCD-A1B1C1D1中，棱AB=BC=3，BB1=4，连接B1C，在CC1上有点E，使得A1C⊥平面EBD，BE交B1C于F．
在边长为a的正方体ABCD-A1B1C1D1中，E、F分别为AB与C1D1的中点．
（1）求证：四边形A1ECF是菱形；
（2）求证：EF⊥平面A1B1C；
（3）求A1B1与平面A1ECF所成角的正切值．
（1）求证：四边形A1ECF是菱形；
（2）求证：EF⊥平面A1B1C；
（3）求A1B1与平面A1ECF所成角的正切值．
如图，M，N，K分别是正方体ABCD-A1B1C1D1的棱AB，CD，C1D1的中点．
如图，已知长方体ABCD-A1B1C1D1，AB=BC=1，BB1=2，连接B1C，过B点作B1C．已知正四棱柱ABCD―A1B1C1D1中，AB=2，AA1=3.
（I）求证：A1C⊥BD；
（II）求直线A1C与侧面BB1C1C所成的角的正切值；
|