题目内容
如图，M，N，K分别是正方体ABCD-A1B1C1D1的棱AB，CD，C1D1的中点．（1）求证：AN∥平面A1MK；
（2）求证：平面A1B1C⊥平面A1MK．
分析：对于（1），要证明AN∥平面A1MK，只需证明AN平行于平面A1MK内的一条直线，容易证明AN∥A1K，从而得到证明；
对于（2），要证明平面A1B1C⊥平面A1MK，只需证明平面A1MK内的直线MK垂直于平面A1B1C即可，而BC1∥MK容易证明，
从而问题得以解决．
对于（2），要证明平面A1B1C⊥平面A1MK，只需证明平面A1MK内的直线MK垂直于平面A1B1C即可，而BC1∥MK容易证明，
从而问题得以解决．
解答：证明：（1）连接KN，由于K、N为CD，C1D1、CD的中点，所以KN平行且等于AA1，
AA1KN为平行四边形?AN∥A1K，而A1K?平面A1MK，AN?平面A1MK，从而AN∥平面A1MK．
（2）连接BC1，由于K、M为AB、C1D1的中点，所以KC1与MB平行且相等，
从而KC1MB为平行四边形，所以MK∥BC1，而BC1⊥B1C，BC1⊥A1B1，从而
BC1⊥平面A1B1C，所以：
?MK⊥面A1B1C?面A1B1C⊥面A1MK．
AA1KN为平行四边形?AN∥A1K，而A1K?平面A1MK，AN?平面A1MK，从而AN∥平面A1MK．
（2）连接BC1，由于K、M为AB、C1D1的中点，所以KC1与MB平行且相等，
从而KC1MB为平行四边形，所以MK∥BC1，而BC1⊥B1C，BC1⊥A1B1，从而
BC1⊥平面A1B1C，所以：
|
点评：本题考查线面平行的判定定理、面面垂直的判定定理的使用，要注意其中的转化思想的应用，
即：将线面平行转化为线线平行，将面面垂直转化为线面垂直．
即：将线面平行转化为线线平行，将面面垂直转化为线面垂直．
练习册系列答案
相关题目
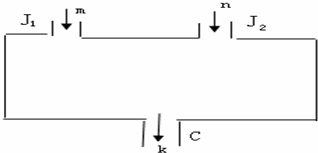21、如图所示，一个计算装置示意图．J1、J2是数据入口，C 是计算结果的出口．计算过程是：由J1、J2 分别输入自然数m和n，经过计算所得结果由出口C输出k，即：f（m，n）=k．此种计算装置满足以下三个性质：①f（1，1）=1；②f（m，n+1）=f（m，n）+2；③f（m+1，1）=2f（m，1）．
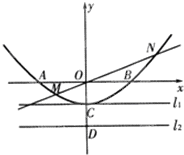如图，已知抛物线与坐标轴分别交于A（-2，0）、B（2，0）、C（0，-1）三点，过坐标原点O的直线y=kx与抛物线交于M、N两点．分别过点C、D（0，-2）、作平行于x轴的直线
如图，这是一个计算机装置示意图，A、B是数据入口处，C是计算机结果的出口，计算过程是由A、B分别输入自然数m和n，经过计算后，得自然数k，由C输出．即：f（m，n）=k，此种计算装置完成计算，满足以下三个性质：①若A、B分别输入1，则输出结果为1，即f（1，1）=1；②若A输入自然数m，B输入自然数由n变为n+1，则输出结果比原来增大2，即f（m，n+1）=f（m，n）+2；③若B输入1，A输入自然数由m变为m+1，则输出结果是原来的2倍，即f（m+1，1）=2f（m，1）．
