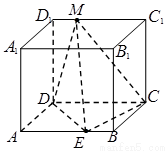题目内容
在边长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB与C1D1的中点.(1)求证:四边形A1ECF是菱形;
(2)求证:EF⊥平面A1B1C;
(3)求A1B1与平面A1ECF所成角的正切值.
分析:(1)取A1B1的中点G,连接C1G、GE.要证四边形A1ECF是菱形,只需证明A1E=A1F=CE=CF即可.
(2)要证EF⊥平面A1B1C,只需证明直线EF垂直平面A1B1C内的两条相交直线A1C、B1C即可;
(3)说明∠B1A1C就是A1B1与平面A1ECF所成的角.然后解三角形,求A1B1与平面A1ECF所成角的正切值.
(2)要证EF⊥平面A1B1C,只需证明直线EF垂直平面A1B1C内的两条相交直线A1C、B1C即可;
(3)说明∠B1A1C就是A1B1与平面A1ECF所成的角.然后解三角形,求A1B1与平面A1ECF所成角的正切值.
解答:(1)证明:取A1B1的中点G,连接C1G、GE.
∵A1G∥FC1且A1G=FC1,∴A1GC1F是平行四边形.
∴A1F∥C1G.同理C1G∥CE.∴A1F∥CE.
由勾股定理算得A1E=A1F=CE=CF=
a,∴四边形A1ECF是菱形.
(2)证明:连接C1B,∵E、F分别为AB与C1D1的中点,
∴C1F=BE.又C1F∥BE,
∴C1FEB为平行四边形.∴C1B∥EF.而C1B⊥B1C,
∴EF⊥B1C.又四边形A1ECF是菱形,∴EF⊥A1C.∴EF⊥面A1B1C.
(3)解:由(2)知,EF⊥平面A1B1C,又EF?平面A1ECF,
∴平面A1B1C⊥平面A1ECF.∴B1在平面A1ECF上的射影在线段A1C上.
∴∠B1A1C就是A1B1与平面A1ECF所成的角.
∵A1B1⊥B1C,在Rt△A1B1C中,tan∠B1A1C=
=
.
∴A1B1与平面A1ECF所成角的正切值为
.
∵A1G∥FC1且A1G=FC1,∴A1GC1F是平行四边形.
∴A1F∥C1G.同理C1G∥CE.∴A1F∥CE.
由勾股定理算得A1E=A1F=CE=CF=
| ||
| 2 |
(2)证明:连接C1B,∵E、F分别为AB与C1D1的中点,
∴C1F=BE.又C1F∥BE,
∴C1FEB为平行四边形.∴C1B∥EF.而C1B⊥B1C,
∴EF⊥B1C.又四边形A1ECF是菱形,∴EF⊥A1C.∴EF⊥面A1B1C.
(3)解:由(2)知,EF⊥平面A1B1C,又EF?平面A1ECF,
∴平面A1B1C⊥平面A1ECF.∴B1在平面A1ECF上的射影在线段A1C上.
∴∠B1A1C就是A1B1与平面A1ECF所成的角.
∵A1B1⊥B1C,在Rt△A1B1C中,tan∠B1A1C=
| B1C |
| A1B1 |
| 2 |
∴A1B1与平面A1ECF所成角的正切值为
| 2 |
点评:本题考查直线与平面垂直的判定,直线与平面平行的判定,直线与平面所成的角,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

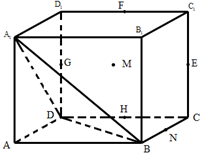 如图,在边长为a的正方体ABCD-A1B1C1D1中,E,F,G,H分别是CC1,C1D1,D1D,CD的中点,N是BC的中点,M在四边形EFGH上及其内部运动,若MN∥平面A1BD,则点M轨迹的长度是
如图,在边长为a的正方体ABCD-A1B1C1D1中,E,F,G,H分别是CC1,C1D1,D1D,CD的中点,N是BC的中点,M在四边形EFGH上及其内部运动,若MN∥平面A1BD,则点M轨迹的长度是 (2009•武汉模拟)(文科做) 如图,在边长为a的正方体ABCD-A1B1C1D1中M、N、P、Q分别为AD,CD,BB1,C1D1的中点
(2009•武汉模拟)(文科做) 如图,在边长为a的正方体ABCD-A1B1C1D1中M、N、P、Q分别为AD,CD,BB1,C1D1的中点