Question

已知正四棱柱ABCD―A₁B₁C­₁D₁中，AB=2，AA₁=3.

（I）求证：A₁C⊥BD；

（II）求直线A₁C与侧面BB₁C₁C所成的角的正切值；

20070406

（III）求二面角B₁―CD―B的正切值.

Answer 1

解：方法一：

(1)    连AC，在正四棱柱ABCD―A₁B₁C₁D₁中，底面ABCD是正方形，

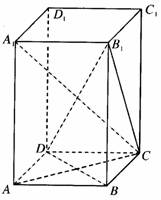
所以AC⊥BD又侧棱AA₁⊥平面ABCD

∴AC是A₁C是平面ABCD内的射影

∴A₁C⊥BD（三垂线定理）

（Ⅱ）在正四棱柱ABCD―A₁B₁C₁D₁中，

A₁B₁⊥平面BB₁C₁C，所以B₁C是A₁C在平面BB₁C₁C内的射影

∴∠A₁CB₁就是直线A₁C与侧面BB₁C₁C所成的角

在直角三角形A₁CB₁中A₁B₁⊥B₁C，A₁B₁=2，B₁C=

（Ⅲ）在正四棱柱ABCD―A₁B₁C₁D₁中，CD⊥平面BB₁C₁C ∴CD⊥B₁C，CD⊥BC

∴∠B₁CB为二面角B₁―CD―B的平面角

二面角B₁―CD―B的的正切值为

方法二：（I）同方法一      

（Ⅱ）如图，以点D为原点建立空间直角坐标系，

   

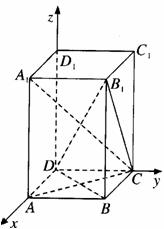
则D（0，0，0），C（0，2，0），A₁（2，0，3）

又在正四棱柱ABCD―A₁B₁C₁D₁中，DC⊥平面BB₁C₁C

为平面BB₁C₁C的一个法向量

又，设直线A₁C与侧面BB₁C₁C所成的角为α，则

 

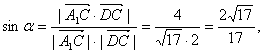
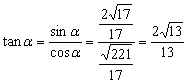即为所求

（Ⅲ）B₁（2，2，3），D₁（0，0，3），B（2，2，0）

在正四棱柱ABCD―A₁B₁C₁D₁中，DD₁⊥平面ABCD，

所以平面ABCD的法向量为=（0，0，3）

设平面B₁DC的法向量为

由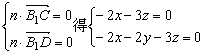

∴n=（3，0，－2）

设二面角B₁―CD―B的大小为θ，则

 

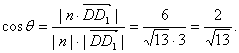
即为所求