题目内容
cos
-tan
+
tan2(-
)+sin
+cos2
+sin
= .
| π |
| 3 |
| 5π |
| 4 |
| 3 |
| 4 |
| π |
| 6 |
| 11π |
| 6 |
| 7π |
| 6 |
| 7π |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:原式中的角度变形后,利用诱导公式及特殊角的三角函数值计算即可得到结果.
解答:
解:原式=cos
-tan
+
tan2
-sin
+cos2
-sin
=
-1+
-
+
-1=-1
.
故答案为:-1
| π |
| 3 |
| π |
| 4 |
| 3 |
| 4 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
故答案为:-1
| 1 |
| 2 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
△ABC 中,
=
,则△ABC一定是( )
| 1-cosA |
| 1-cosB |
| a |
| b |
| A、钝角三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、等腰三角形 |
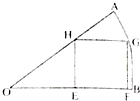 如图所示,扇形OAB中,∠AOB=
如图所示,扇形OAB中,∠AOB=