题目内容
如图所示，在连接正八边形的三个顶点而成的三角形中，与正八边形有公共边的三角形有多少个．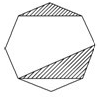
考点：计数原理的应用
专题：计算题,排列组合
分析：把与正八边形有公共边的三角形分为两类：有一条公共边的三角形、有两条公共边的三角形，由分类加法计数原理，可得结论．
解答：
解：把与正八边形有公共边的三角形分为两类：
第一类，有一条公共边的三角形共有8×4=32（个）；
第二类，有两条公共边的三角形共有8（个）．
由分类加法计数原理知，共有32+8=40（个）．
第一类，有一条公共边的三角形共有8×4=32（个）；
第二类，有两条公共边的三角形共有8（个）．
由分类加法计数原理知，共有32+8=40（个）．
点评：本题考查由分类加法计数原理，考查学生分析解决问题的能力，正确分类是关键．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
相关题目
设f（x）=xlnx，若f′（x0）=1，则x0=（ ）
| A、e2 | B、1 |
| C、e | D、ln2 |
下列说法正确的是（ ）
| A、若a＞b，c＞d，则ac＞bd | ||||
B、若
| ||||
| C、若b＞c，则|a|•b≥|a|•c | ||||
| D、若a＞b，c＞d，则a-c＞b-d |
下列有关命题的说法中错误的是（ ）
| A、若“p或q”为假命题，则p、q均为假命题 | ||||||||||||||||
B、命题“若
| ||||||||||||||||
C、“sinx=
| ||||||||||||||||
| D、若命题p：“存在实数x使x2≥0”，则命题p的否定为“对于任意x∈R都有x2＜0” |