题目内容
函数y=2-|x-1|-m的图象与x轴有交点时，m的范围是（ ）
| A、-1≤m＜0 | B、0≤m≤1 |
| C、m≥1 | D、0＜m≤1 |
考点：函数的零点
专题：函数的性质及应用
分析：将函数的解得问题转化为方程的根的问题，得0＜2-|x-1|≤20=1，从而问题解决．
解答：
解：函数y=2-|x-1|-m的图象与x轴有交点，
即y=0有解，即2-|x-1|=m有解；
∵-|x-1|≤0，
∴0＜2-|x-1|≤20=1，
∴0＜m≤1，
故选：D．
即y=0有解，即2-|x-1|=m有解；
∵-|x-1|≤0，
∴0＜2-|x-1|≤20=1，
∴0＜m≤1，
故选：D．
点评：本题考查了函数的零点问题，考查转化思想，是一道基础题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
函数f（x）的图象如图所示，下列数值排序正确的是（ ）
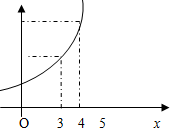
| A、0＜f′（3）＜f′（4）＜f（4）-f（3） |
| B、0＜f′（3）＜f（4）-f（3）＜f′（4） |
| C、0＜f′（4）＜f′（3）＜f（4）-f（3） |
| D、0＜f（4）-f（3）＜f′（3）＜f′（4） |
有一段“三段论”推理：对于可导函数f（x），若f（x）在区间（a，b）上是增函数，则f′（x）＞0对x∈（a，b）恒成立，因为函数f（x）=x3在R上是增函数，所以f（x）=3x2＞0对x∈R恒成立．以上推理中（ ）
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、推理正确 |
不等式log3|x-
|＜-1的解集是（ ）
| 1 |
| 3 |
A、（0，
| ||||||
B、（
| ||||||
C、（0，
| ||||||
D、（
|
设函数y=f（x），x∈[a，b]，其导函数的图象如图所示，则函数y=f（x）的减区间是（ ）
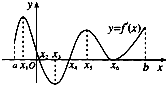
| A、（x1，x3） |
| B、（x2，x4） |
| C、（x4，x6） |
| D、（x5，x6） |