题目内容
12.已知tan(α+β)=-2,tan(α-β)=$\frac{1}{2}$,求$\frac{sin2α}{sin2β}$的值.分析 利用角的变换,和差的三角函数,弦化切,即可求$\frac{sin2α}{sin2β}$的值.
解答 解:∵tan(α+β)=-2,tan(α-β)=$\frac{1}{2}$,
∴$\frac{sin2α}{sin2β}$=$\frac{sin[(α+β)+(α-β)]}{sin[(α+β)-(α-β)]}$=$\frac{sin(α+β)cos(α-β)+cos(α+β)sin(α-β)}{sin(α+β)cos(α-β)-cos(α+β)sin(α-β)}$=$\frac{tan(α+β)+tan(α-β)}{tan(α+β)-tan(α-β)}$=$\frac{-2+\frac{1}{2}}{-2-\frac{1}{2}}$=$\frac{3}{5}$.
点评 本题考查角的变换,和差的三角函数,弦化切,考查学生的计算能力,正确转化是关键.

练习册系列答案
相关题目
7.已知集合A={x|x2-4x+3<0},B={x|2<x<4},则A∩B=( )
| A. | (1,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |

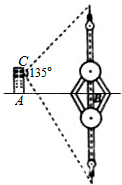 如图所示,某人居住在离地面100米处的楼房C处,测得平静江河的对面转播塔尖以及转播塔的倒影中的塔尖的张角为135°,又知楼房离转播塔的距离AB=200m,试问:能否推算出转播塔的高度?若能,请确定塔高;若不能,请说明理由.
如图所示,某人居住在离地面100米处的楼房C处,测得平静江河的对面转播塔尖以及转播塔的倒影中的塔尖的张角为135°,又知楼房离转播塔的距离AB=200m,试问:能否推算出转播塔的高度?若能,请确定塔高;若不能,请说明理由.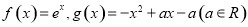 ,点
,点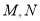 分别在
分别在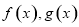 的图象上.
的图象上.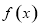 在
在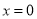 处的切线恰好与
处的切线恰好与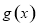 相切,求
相切,求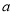 的值;
的值; 的横坐标均为
的横坐标均为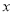 ,记
,记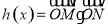 ,当
,当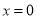 时,函数
时,函数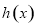 取得极大值,求
取得极大值,求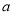 的范围.
的范围.