题目内容
设函数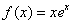 .
.
(1) 求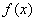 的单调区间与极值;
的单调区间与极值;
(2)是否存在实数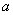 ,使得对任意的
,使得对任意的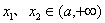 ,当
,当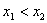 时恒有
时恒有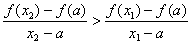 成立.若存在,求
成立.若存在,求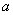 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
(1)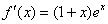 .令
.令 ,得
,得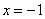 ; 列表如下
; 列表如下
|
|
|
|
|
|
| - | 0 | + |
|
|
| 极小值 |
|
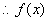 的单调递减区间是
的单调递减区间是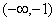 ,单调递增区间是
,单调递增区间是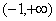 .
.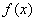 极小值=
极小值=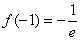
(2) 设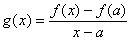 ,由题意,对任意的
,由题意,对任意的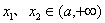 ,当
,当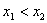 时恒有
时恒有
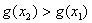 ,即
,即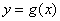 在
在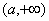 上是单调增函数.
上是单调增函数.
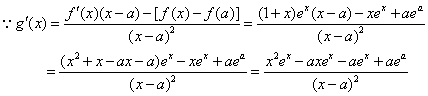
 ,
,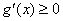 令
令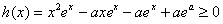
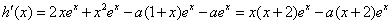
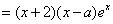
若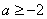 ,当
,当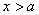 时,
时,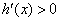 ,
,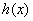 为
为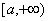 上的单调递增函数,
上的单调递增函数,
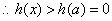 ,不等式成立.
,不等式成立.
若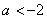 ,当
,当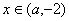 时,
时,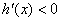 ,
,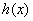 为
为 上的单调递减函数,
上的单调递减函数,
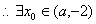 ,
,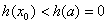 ,与
,与 ,
,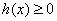 矛盾
矛盾
所以,a的取值范围为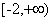 .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
根据如下样本数据
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | 2.5 |
| 0.5 |
|
得到的回归方程为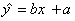 .若
.若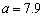 ,则
,则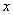 每增加1个单位,
每增加1个单位,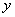 就 ( )
就 ( )
A.增加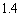 个单位; B.减少
个单位; B.减少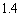 个单位; C.增加
个单位; C.增加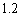 个单位; D.减少
个单位; D.减少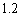 个单位.
个单位.
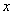
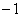
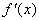



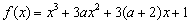 有极值,则
有极值,则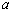 的取值范围是__
的取值范围是__  ,且
,且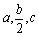 成等差数列.若其对角线长为
成等差数列.若其对角线长为 ,则
,则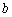 的最大值为________.
的最大值为________. 上的任意函数
上的任意函数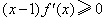 ,则必有 ( )
,则必有 ( )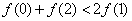 B.
B.
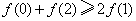 D.
D.
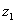 满足
满足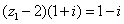 (
(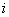 为虚数单位),复数
为虚数单位),复数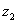 的虚部为
的虚部为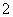 ,
,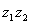 是实数,求
是实数,求 0.5
0.5 ,
, .
. 的图象关于直线
的图象关于直线 对称,求
对称,求 的最小值;
的最小值; 在
在 上有零点,求实数
上有零点,求实数 的取值范围.
的取值范围. ,
, .
. 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围; 的最小值;
的最小值; 时,若
时,若 与
与 的图象有两个交点
的图象有两个交点 ,求证:
,求证:
 .
. 为
为 ,取
,取 为
为 ,取
,取 为
为 )
) 时,求k的值.
时,求k的值.