题目内容
对于 上的任意函数
上的任意函数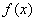 ,若满足
,若满足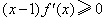 ,则必有 ( )
,则必有 ( )
A.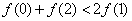 B.
B.
C.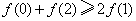 D.
D.
C

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
题目内容
对于 上的任意函数
上的任意函数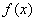 ,若满足
,若满足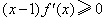 ,则必有 ( )
,则必有 ( )
A.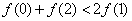 B.
B.
C.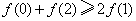 D.
D.
C

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案