题目内容
已知抛物线y2=-x与直线y=k(x+1)相交于A、B两点.
(1)求证:OA⊥OB;
(2)当△OAB的面积等于 时,求k的值.
时,求k的值.

解 设A(x1,y1)、B(x2,y2).
 (1)由
(1)由 得ky2+y-k=0,(2分)
得ky2+y-k=0,(2分)
∴y1y2=-1.又-x1=y ,-x2=y
,-x2=y ,
,
∴x1x2=(y1y2)2=1,∴x1x2+y1y2=0.(4分)
∴ ·
· =x1x2+y1y2=0,
=x1x2+y1y2=0,
∴OA⊥OB.(6分)
(2)如图,由(1)知y1+y2=- ,
,
y1y2=-1,
∴|y1-y2|=

=  =2
=2 ,(10分)
,(10分)
∴k2= ,∴k=±
,∴k=± ,
,
即所求k的值为± .(13分)
.(13分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
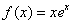 .
.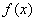 的单调区间与极值;
的单调区间与极值;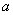 ,使得对任意的
,使得对任意的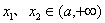 ,当
,当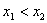 时恒有
时恒有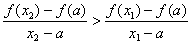 成立.若存在,求
成立.若存在,求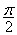 ;
; 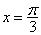 对称;
对称; 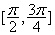 上为减函数.
上为减函数.  B.
B. C.
C. D.
D.
 有零点的概率为___________.
有零点的概率为___________.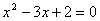 ,则
,则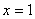 ”的逆否命题为“若
”的逆否命题为“若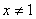 ,则
,则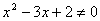 ”
”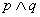 为假命题,则
为假命题,则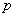 、
、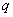 均为假命题
均为假命题 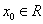 ,使得
,使得 ,则
,则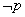 :任意
:任意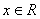 ,都有
,都有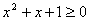
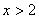 ”是“
”是“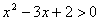 ”的充分不必要条件
”的充分不必要条件 的图象向左平移
的图象向左平移 个单位, 再向上平移1个单位,所得图象的函数解析式是( ).
个单位, 再向上平移1个单位,所得图象的函数解析式是( ). B.
B.
 D.
D.
 满足
满足 ,则
,则