题目内容
已知函数 ,
, .
.
(1)若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2) 若直线 是函数
是函数 图象的切线,求
图象的切线,求 的最小值;
的最小值;
(3)当 时,若
时,若 与
与 的图象有两个交点
的图象有两个交点 ,求证:
,求证:
 .
.
(取 为
为 ,取
,取 为
为 ,取
,取 为
为 )
)
解:(1)
 ,则
,则 ,
,
∵ 在
在 上单调递增,∴对
上单调递增,∴对 ,都有
,都有 ,
,
即对 ,都有
,都有 ,∵
,∵ ,∴
,∴ ,故实数
,故实数 的取值范围是
的取值范围是 .
.
(2) 设切点 ,则切线方程为
,则切线方程为 ,
,
即 ,亦即
,亦即 ,
,
令 ,由题意得
,由题意得 ,……7分
,……7分
令 ,则
,则 ,
,
当 时 ,
时 , ,
, 在
在 上单调递减;
上单调递减;
当 时,
时, ,
, 在
在 上单调递增,
上单调递增,
∴ ,故
,故 的最小值为
的最小值为 . ………………10分
. ………………10分
(3)由题意知 ,
, ,
,
两式相加得 ,两式相减得
,两式相减得 ,
,
即 ,∴
,∴ ,
,
即 , …………12分
, …………12分
不妨令 ,记
,记 ,令
,令 ,则
,则 ,
,
∴ 在
在 上单调递增,则
上单调递增,则 ,
,
∴ ,则
,则 ,∴
,∴ ,
,
又 ,
,
∴ ,即
,即 ,
,
令 ,则
,则 时,
时, ,∴
,∴ 在
在 上单调递增,
上单调递增,
又 ,
,
∴ ,则
,则 ,即
,即 .
.

练习册系列答案
相关题目
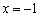 ,则
,则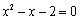 ”的逆否命题是
”的逆否命题是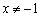 ,则
,则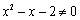 B.若
B.若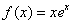 .
.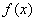 的单调区间与极值;
的单调区间与极值;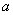 ,使得对任意的
,使得对任意的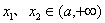 ,当
,当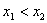 时恒有
时恒有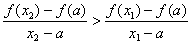 成立.若存在,求
成立.若存在,求 满足
满足 ,则
,则 =( )
=( ) B.
B.  C.
C. D.
D.
 与抛物线
与抛物线 (
( 重合,
重合,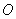 为原点,点
为原点,点 是抛物线准线上一动点,点
是抛物线准线上一动点,点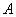 在抛物线上,且
在抛物线上,且 ,则
,则 的最小值为
的最小值为  的零点一定位于区间( )
的零点一定位于区间( ) 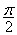 ;
; 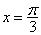 对称;
对称; 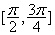 上为减函数.
上为减函数.  B.
B. C.
C. D.
D.
 满足
满足 ,则
,则