题目内容
△ABC中，AB=
，AC=1，∠B=30°，则∠C等于
- A.60°
- B.90°
- C.120°
- D.60°或120°
D
分析：由B的度数求出sinB的值，再由AB，AC的值，利用正弦定理求出sinC的值，根据C的范围，利用特殊角的三角函数值即可求出角C的度数．
解答：由AB=，AC=1，∠B=30°，
根据正弦定理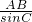
=
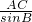得：sinC=
=
=
，
又AB＞AC，得到∠C＞∠B，即30°＜∠C＜180°，
则∠C=60°或120°．
故选D
点评：此题属于解三角形的题型，涉及的知识有正弦定理，三角形边角的关系，以及特殊角的三角函数值，根据正弦定理求出sinC的值是解本题的关键，同时注意判断得出角C的具体范围．
分析：由B的度数求出sinB的值，再由AB，AC的值，利用正弦定理求出sinC的值，根据C的范围，利用特殊角的三角函数值即可求出角C的度数．
解答：由AB=
，AC=1，∠B=30°，根据正弦定理
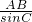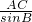=得：sinC===，又AB＞AC，得到∠C＞∠B，即30°＜∠C＜180°，
则∠C=60°或120°．
故选D
点评：此题属于解三角形的题型，涉及的知识有正弦定理，三角形边角的关系，以及特殊角的三角函数值，根据正弦定理求出sinC的值是解本题的关键，同时注意判断得出角C的具体范围．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC中，AB=4，AC=8，∠BAC=60°，延长CB到D，使BA=BD，当E点在线段AB上移动时，若在△ABC中，AB=7，BC=5，CA=6，则
•
=（ ）
| AB |
| BC |
| A、-19 | B、19 |
| C、-38 | D、38 |
△ABC中，AB=4，AC=4