题目内容
如图，△ABC中，AB=4，AC=8，∠BAC=60°，延长CB到D，使BA=BD，当E点在线段AB上移动时，若| AE |
| AC |
| AD |
分析：由题意知，当λ取最大值时，点E与点B重合．△ABC中，由余弦定理求得BC 的值，根据λ=
，μ=
，求出 λ和μ 的值，从而得到λ-μ的值．
| DB |
| DC |
| CB |
| CD |
解答：解：如图所示：设AM∥BN，且 AM=BN，由题意知，当λ取最大值时，点E与点B重合．△ABC中，由余弦定理
求得BC=
=4
．
又∵
=λ
+μ
，∴λ=
=
=
=
，
μ=
=
=
=
，λ-μ=
-2，
故答案为：
-2．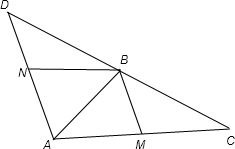
求得BC=
| 16 +64 - 2×4×8cos60° |
| 3 |
又∵
| AE |
| AC |
| AD |
| AM |
| AC |
| DB |
| DC |
| 4 | ||
4+4
|
| ||
| 2 |
μ=
| AN |
| AD |
| CB |
| CD |
4
| ||
4+4
|
3-
| ||
| 2 |
| 3 |
故答案为：
| 3 |
点评：本题考查余弦定理，两个向量的加减法的法则，以及其几何意义，判断当λ取最大值时，点E与点B重合，是解题的突破口，求出 λ和μ 的值，是解题的关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
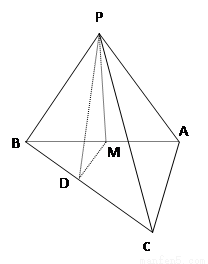
如图，△ABC中，∠A=90°，AB=4，AC=3，平面ABC外一点P在平面ABC内的射影是AB中点M，二面角P-AC-B的大小为45°．
如图在△ABC中，AB⊥AC，
