题目内容
圆x2+y2-6x+7=0上的点到直线x-y+1=0距离的最小值为( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、3
|
考点:直线与圆的位置关系
专题:直线与圆
分析:求出圆心到直线x-y+1=0的距离d,由d-r即可求出P到直线距离的最小值.
解答:
解:由圆方程得:圆心(3,0),半径r=
,
∵圆心到直线x-y+1=0的距离d=
=2
,
∴动点P到直线x-y+1=0的距离的最小值等于d-r=2
-
=
;
故选A.
| 2 |
∵圆心到直线x-y+1=0的距离d=
| |3-0+1| | ||
|
| 2 |
∴动点P到直线x-y+1=0的距离的最小值等于d-r=2
| 2 |
| 2 |
| 2 |
故选A.
点评:此题考查了直线与圆的位置关系,点到直线的距离公式,圆的标准方程,根据题意得出动点P到直线x-y+1=0的距离的最小值为d-r是解本题的关键.

练习册系列答案
相关题目
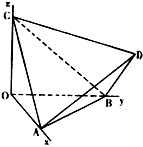 如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )
如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )| A、O-ABC是正三棱锥 |
| B、直线AD与OB所成的角是45° |
| C、直线OB∥平面ACD |
| D、二面角D-OB-A为45° |
已知y=f(x)是偶函数,当x>0时,f(x)=x+
,且x∈[-3,-1]时n≤f(x)≤m恒成立,则m-n的最小值是( )
| 4 |
| x |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
已知定点A(2014,2),F是抛物线y2=2x的焦点,点P是抛物线上的动点,当|PA|+|PF|最小时,点P的坐标为( )
| A、(0,0) | ||
B、(1,
| ||
| C、(2,2) | ||
D、(
|