题目内容
已知方程|xex|=t有三个不相等的实数解,则t的取值范围是 .
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:方程|xex|=t有三个不相等的实数解,即y=t与函数y=|xex|的图象有三个交点,利用导数法分析f(x)=xex的单调性和极值,进而结合函数图象的对折变换画出函数y=|xex|的图象,数形结合可得答案.
解答:
解:令f(x)=xex,则f′(x)=(1+x)ex,
当x<-1时,f′(x)<0,当x>-1时,f′(x)>0,
故f(x)=xex在(-∞,-1)上为减函数,在(-1,+∞)上是减函数,
f(-1)=-
,
又由x<0时,f(x)<0,当x>0时,f(x)>0,
故函数y=|xex|的图象如下图所示:
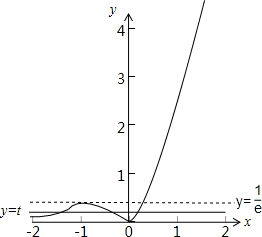
故当t∈(0,
)时,y=t与函数y=|xex|的图象有三个交点,
即方程|xex|=t有三个不相等的实数解,
故t的取值范围是(0,
),
故答案为:(0,
)
当x<-1时,f′(x)<0,当x>-1时,f′(x)>0,
故f(x)=xex在(-∞,-1)上为减函数,在(-1,+∞)上是减函数,
f(-1)=-
| 1 |
| e |
又由x<0时,f(x)<0,当x>0时,f(x)>0,
故函数y=|xex|的图象如下图所示:

故当t∈(0,
| 1 |
| e |
即方程|xex|=t有三个不相等的实数解,
故t的取值范围是(0,
| 1 |
| e |
故答案为:(0,
| 1 |
| e |
点评:本题考查的知识点是根的存在性及根的个数,其中结合函数图象的对折变换画出函数y=|xex|的图象,是解答的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
已知q:5>2,p:3+3=5,则下列判断错误的是( )
| A、“p或q”为真,“非q”为假 |
| B、“p且q”为假,“非p”为假 |
| C、“p且q”为假,“非p”为真 |
| D、“p且q”为假,“p或q”为真 |