题目内容
已知函数f(x)=x(ex-1)-ax2.
(Ⅰ)若f(x)在x=-1时有极值,求a的值及函数f(x)的单调递减区间;
(Ⅱ)当x≥0时,f(x)≥0,求a的取值范围.
(Ⅰ)若f(x)在x=-1时有极值,求a的值及函数f(x)的单调递减区间;
(Ⅱ)当x≥0时,f(x)≥0,求a的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由已知得f'(x)=ex-1+xex-2ax.由此利用导数性质能求出函数f(x)的单调递减区间.
(Ⅱ)法一:令g(x)=xa-1-ax,则g'(x)=ex-a.由此利用分类讨论思想和导数性质能求出实数a的取值范围.
(Ⅱ)法二:当x≥0时,x(ex-1)≥ax2.由此利用分类讨论思想和导数性质能求出实数a的取值范围.
(Ⅱ)法一:令g(x)=xa-1-ax,则g'(x)=ex-a.由此利用分类讨论思想和导数性质能求出实数a的取值范围.
(Ⅱ)法二:当x≥0时,x(ex-1)≥ax2.由此利用分类讨论思想和导数性质能求出实数a的取值范围.
解答:
(Ⅰ)解:f'(x)=ex-1+xex-2ax.由f'(-1)=0得,a=
…2分
当
=
时,f(x)=x(ex-1)-
x2,
f'(x)=ex-1+xex-x=(ex-1)(x+1)
当x∈(-∞,-1)时f'(x)>0;
当x∈(-1,0)时,f'(x)<0;当x∈(0,+∞)时,f'(x)>0.
故f(x)在(-∞,-1),(0,+∞)单调增加,在(-1,0)单调减少,
则f(x)在x=-1时有极小值,所以a=
,
函数f(x)的单调递减区间为(-1,0).…6分
(Ⅱ)解法一:f(x)=x(xa-1-ax).
令g(x)=xa-1-ax,则g'(x)=ex-a.
若a≤1,则当x∈(0,+∞)时,g'(x)>0,g(x)为减函数,
而g(0)=0,从而当x≥0时g(x)≥0,即f(x)≥0.…9分
若a>1,则当x∈(0,lna)时,g'(x)<0,g(x)为减函数,
而g(0)=0,从而当x∈(0,lna)时g(x)<0,即f(x)<0.…11分
综合得a的取值范围为(-∞,1]…12分
(Ⅱ)解法二:当x≥0时,f(x)≥0,即x(ex-1)≥ax2.
①当x=0时,a∈R; …7分
②当x>0时,x(ex-1)≥ax2等价于ex-1≥ax,也即a≤
.
记g(x)=
,x∈(0,+∞),
则g′(x)=
.…8分
记h(x)=(x-1)ex+1,x∈(0,+∞),
则h′(x)=xex>0,因此h(x)=(x-1)ex+1在(0,+∞)上单调递增,
且h(x)>h(0)=0,所以g′(x)=
>0,
从而g(x)=
在(0,+∞)上单调递增.…9分
由洛必达法则有
g(x)=
=
=1,
即当x→0时,g(x)→1
所以g(x)>1,即有a≤1.…11分
综上①、②所述,a的取值范围为(-∞,1]…12分.
| 1 |
| 2 |
当
 |
| AC |
 |
| BD |
| 1 |
| 2 |
f'(x)=ex-1+xex-x=(ex-1)(x+1)
当x∈(-∞,-1)时f'(x)>0;
当x∈(-1,0)时,f'(x)<0;当x∈(0,+∞)时,f'(x)>0.
故f(x)在(-∞,-1),(0,+∞)单调增加,在(-1,0)单调减少,
则f(x)在x=-1时有极小值,所以a=
| 1 |
| 2 |
函数f(x)的单调递减区间为(-1,0).…6分
(Ⅱ)解法一:f(x)=x(xa-1-ax).
令g(x)=xa-1-ax,则g'(x)=ex-a.
若a≤1,则当x∈(0,+∞)时,g'(x)>0,g(x)为减函数,
而g(0)=0,从而当x≥0时g(x)≥0,即f(x)≥0.…9分
若a>1,则当x∈(0,lna)时,g'(x)<0,g(x)为减函数,
而g(0)=0,从而当x∈(0,lna)时g(x)<0,即f(x)<0.…11分
综合得a的取值范围为(-∞,1]…12分
(Ⅱ)解法二:当x≥0时,f(x)≥0,即x(ex-1)≥ax2.
①当x=0时,a∈R; …7分
②当x>0时,x(ex-1)≥ax2等价于ex-1≥ax,也即a≤
| ex-1 |
| x |
记g(x)=
| ex-1 |
| x |
则g′(x)=
| (x-1)ex+1 |
| x |
记h(x)=(x-1)ex+1,x∈(0,+∞),
则h′(x)=xex>0,因此h(x)=(x-1)ex+1在(0,+∞)上单调递增,
且h(x)>h(0)=0,所以g′(x)=
| h(x) |
| x |
从而g(x)=
| ex-1 |
| x |
由洛必达法则有
| lim |
| x→0 |
| lim |
| x→0 |
| ex-1 |
| x |
| lim |
| x→0 |
| ex |
| 1 |
即当x→0时,g(x)→1
所以g(x)>1,即有a≤1.…11分
综上①、②所述,a的取值范围为(-∞,1]…12分.
点评:本题主要考查函数、导数等基本知识.考查运算求解能力及化归思想、函数方程思想、分类讨论思想的合理运用,注意导数性质的合理运用.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
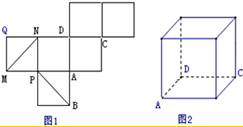 图1是一个正方体的表面展开图,MN和PB是两条面对角线,请在图2的正方体中将MN和PB画出来,并就这个正方体解决下列问题
图1是一个正方体的表面展开图,MN和PB是两条面对角线,请在图2的正方体中将MN和PB画出来,并就这个正方体解决下列问题 如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).
如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).