题目内容
已知集合A={x|
＜1，x∈R}，集合B是函数y=lg（x+1）的定义域，则A∩B= ．
| 1 |
| x |
考点：交集及其运算,函数的定义域及其求法
专题：集合
分析：求出A中不等式的解集确定出A，求出函数的定义域确定出，找出两集合的交集即可．
解答：
解：当x＞0时，A中不等式去分母得x＞1，即A=（1，+∞）；
当x＜0，A中不等式去分母得：x＜1，即A=（-∞，0），
∴A=（-∞，0）∪（1，+∞），
由B中y=lg（x+1），得到x+1＞0，即x＞-1，
∴B=（-1，+∞），
则A∩B=（-1，0）∪（1，+∞）．
故答案为：（-1，0）∪（1，+∞）
当x＜0，A中不等式去分母得：x＜1，即A=（-∞，0），
∴A=（-∞，0）∪（1，+∞），
由B中y=lg（x+1），得到x+1＞0，即x＞-1，
∴B=（-1，+∞），
则A∩B=（-1，0）∪（1，+∞）．
故答案为：（-1，0）∪（1，+∞）
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
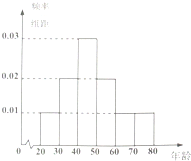“行通济”是广东佛山一带在元宵节期间举行的游玩祈福活动，每到这一天，家家户户都会扶老携幼，自清晨到夜幕，举着风车、摇着风铃、拎着生菜浩浩荡荡地由北到南走过通济桥，祈求来年平平安安、顺顺利利．为了了解不同年龄层次的人对这一传统习俗的参与度，现随机抽取年龄在20～80岁之间的60人，并按年龄层次[20，30），[30，40），[40，50），[50，60），[60，70），[70，80）绘制频率分布直方图如图所示，其中参与了2014年“行通济”活动的人数如下表．若规定年龄分布在[20，60）岁的为“中青年人”，60岁以上（含60岁）为“老年人”．下列说法正确的是（ ）
| A、命题“若x2=1，x=1”的否命题是“若x2=1，则x≠1” | ||
| B、“x=-1”是“x2-x-2=0”的必要不充分条件 | ||
| C、命题“若x=y，则sinx=siny”的逆否命题是真命题 | ||
D、“tanx=1”是“x=
|