题目内容

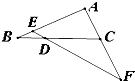如图，在△ABC中，已知点D是BC边的三等分点且BD=
1
3
BC，过点D的直线分别交直线AB，AC于E，F两点，若
AE
=λ
AB
（λ＞0），
AF
=μ
AC
（μ＞0），则λ+2μ的最小值为
 
．
考点：平面向量的基本定理及其意义
专题：导数的综合应用,平面向量及应用
分析：由已知条件，
EB
=
ED
+
DB
=(1-λ)
AB
，而
ED
=-kλ
AB
+kμ
AC
，
DB
=
1
3
AB
-
1
3
AC
，所以得到(
1
3
-kλ)
AB
+(kμ-
1
3
)
AC
=(1-λ)
AB
．从而得到
1
3
-kλ=1-λ
kμ-
1
3
=0
，消去k并求得μ=
λ
3λ-2
，所以λ+2μ=λ+
2λ
3λ-2
，通过求导求关于λ的函数λ+
2λ
3λ-2
的最小值即可．
解答： 解：
EB
=
ED
+
DB
=(1-λ)
AB
；
E，D，F三点共线，∴存在实数k，使
ED
=k
EF
=k(
AF
-
AE
)=-kλ
AB
+kμ
AC
，
DB
=
1
3
CB
=
1
3
AB
-
1
3
AC
；
∴(
1
3
-kλ)
AB
+(kμ-
1
3
)
AC
=(1-λ)
AB
；
∴
1
3
-kλ=1-λ		①
kμ-
1
3
=0		②
；
由②得，k=
1
3μ
带入①得，
1
3
-
λ
3μ
=1-λ；
∴μ=
λ
3λ-2
；
∴λ+2μ=λ+
2λ
3λ-2
；
设f（λ）=λ+
2λ
3λ-2
，λ＞0；
∴f′(λ)=
9λ2-12λ
(3λ-2)2
，令f′（λ）=0得，λ=0，或
4
3
；
∴λ∈(0，
4
3
)时，f′（λ）＜0，λ∈(
4
3
，+∞)时，f′（λ）＞0；
∴λ=
4
3
时，f（λ）取极小值，也是最小值；
∴f（λ）的最小值为
8
3
；
即λ+2μ的最小值为
8
3
．
故答案为：
8
3
．
点评：考查向量的加法、减法运算，共线向量基本定理，以及平面向量基本定理，通过求导求函数的最小值的方法及过程．
练习册系列答案
相关题目
过点P（-2，1）作两条斜率互为相反数的直线，分别与抛物线x2=4y交于A，B两点，若直线AB与圆C：x2+（y-1）2=1交于不同两点M，N，则|MN|的最大值是
 
．
已知函数f（x）=|x-2|，g（x）=-|x+3|+m．
（1）若关于x的不等式g（x）≥0的解集为[-5，-1]，求实数m的值；
（2）若f（x）的图象恒在g（x）图象的上方，求实数m的取值范围．
已知函数g（x）=ax2-2a+1+b（a＞0）在区间[2，3]上头最大值4和最小值1，设f（x）=
g(x)
x

（1求a，b的值
（2）若不等式f（2x）-k.2x≥0在x∈[-1，1]有解，求实数k的取值范围．
已知双曲线3x2-y2=12的中心为O，左右焦点分别为F1，F2，左顶点为A．
（1）求双曲线的实轴长、虚轴长、离心率和渐近线方程；
（2）设过A平行于y轴的直线交双曲线的两条渐近线分别于B，C，求四边形F1COB的面积．
求曲线y=f（x）=
1
2
x2-3x+2lnx在（3，f（3））处切线的斜率及切线方程．
设命题p：c2＜c和命题q：?x∈R，x2+4cx+1＞0，若p真q假，则实数c的取值范围是
 
．
（1）根据下面的要求，求S=13+23+…+1023值．请完成执行该问题的程序框图．
（2）请运用更相减损术求459与357的最大公约数．
已知函数f（x）满足：（1）对于任意的x1，x2∈R，有f（x1+x2）=f（x1）•f（x2）；（2）满足“对任意x1，x2∈R，且x1≠x2，都有
f(x1)-f(x2)
x1-x2
＜0”，下列函数满足这些条件的函数是（　　）
A、f（x）=lnx
B、f（x）=x 
1
3
C、f（x）=ax（0＜a＜1）
D、f（x）=ax（a＞1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网