题目内容
已知
=（sinωx+cosωx，
cosωx），
=（cosωx-sinωx，2sinωx）（ω＞0）．若f（x）=
•
，且f（x）相邻两对称轴间的距离等于
．
（1）求ω的值；
（2）在△ABC中，a，b，c分别是角A，B，C的对边，a=
，b+c=3（b＞c），f（A）=1，求边b，c的长．
| m |
| 3 |
| n |
| m |
| n |
| π |
| 2 |
（1）求ω的值；
（2）在△ABC中，a，b，c分别是角A，B，C的对边，a=
| 3 |
考点：三角函数中的恒等变换应用,正弦定理
专题：三角函数的图像与性质
分析：（1）首先，结合平面向量数量积的坐标运算，化简函数f（x）的解析式，然后，结合周期公式，确定ω的值；
（2）根据（1），先确定A的值，然后，结合余弦定理，求解边b，c的长．
（2）根据（1），先确定A的值，然后，结合余弦定理，求解边b，c的长．
解答：
解：（1）∵
=（sinωx+cosωx，
cosωx），
=（cosωx-sinωx，2sinωx）（ω＞0），
∴f（x）=
•
=
=
，
∵T=
=
，
∴ω=1，
∴ω的值1．
（2）由（1）ω=1，
∴f(x)=2sin(2x+
)，
∵f（A）=1，∴sin(2A+
)=
，
而
＜2A+
＜
，
∴2A+
=
π，
∴A=
．
由余弦定理：cosA=
=
，
即b2+c2-bc=3，又b+c=3，（b＞c）
联立解得：b=2，c=1．
| m |
| 3 |
| n |
∴f（x）=
| m |
| n |
|
=
|
∵T=
| π |
| 2ω |
| π |
| 2 |
∴ω=1，
∴ω的值1．
（2）由（1）ω=1，
∴f(x)=2sin(2x+
| π |
| 6 |
∵f（A）=1，∴sin(2A+
| π |
| 6 |
| 1 |
| 2 |
而
| π |
| 6 |
| π |
| 6 |
| 13π |
| 6 |
∴2A+
| π |
| 6 |
| 5 |
| 6 |
∴A=
| π |
| 3 |
由余弦定理：cosA=
| 1 |
| 2 |
| b2+c2-a2 |
| 2bc |
即b2+c2-bc=3，又b+c=3，（b＞c）
联立解得：b=2，c=1．
点评：本题综合考查了三角恒等变换公式，二倍角公式等知识，余弦定理及其运用等，属于中档题．
练习册系列答案
相关题目
若（x-
）n的展开式中第2项与第4项的二项式系数相等，则直线y=nx与曲线y=x2围成的封闭区域面积为（ ）
| 2 |
| x |
A、
| ||
| B、12 | ||
C、
| ||
| D、36 |
若随机变量ξ～B（n，P），且Eξ=6，Dξ=3，则P（ξ=1）的值为（ ）
| A、3•2-2 |
| B、3•2-10 |
| C、2-4 |
| D、2-8 |
已知sin（θ-
）=2cos（θ+
），则
=（ ）
| π |
| 4 |
| π |
| 4 |
sin(
| ||
sin(
|
| A、-4 | ||
| B、-2 | ||
C、
| ||
| D、-1 |
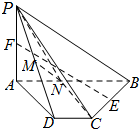如图所示，四棱锥P-ABCD中，PA⊥面ABCD，AB∥CD，∠ABC=90°，AP=BC=2，AB=3，CD=1，E、F、M分别是BC、PA、PD的中点．