题目内容
2011是等差数列：1，4，7，10…的第（ ）项．
| A、669 | B、670 |
| C、671 | D、672 |
考点：数列的概念及简单表示法
专题：点列、递归数列与数学归纳法
分析：由等差数列：1，4，7，10…可得首项a1=1，公差d=4-1=3，即可得出通项公式an．令an=2011解出即可．
解答：
解：由等差数列：1，4，7，10…
可得首项a1=1，公差d=4-1=3，
∴通项公式an=a1+（n-1）d=1+3（n-1）=3n-2．
令3n-2=2011，解得n=671．
∴2011是等差数列：1，4，7，10…的第671项．
故选：C．
可得首项a1=1，公差d=4-1=3，
∴通项公式an=a1+（n-1）d=1+3（n-1）=3n-2．
令3n-2=2011，解得n=671．
∴2011是等差数列：1，4，7，10…的第671项．
故选：C．
点评：本题考查了等差数列的通项公式，属于基础题．
练习册系列答案
相关题目
用10元、5元和1元来支付20元钱的书款，不同的支付方法有（ ）
| A、3 | B、5 | C、9 | D、12 |
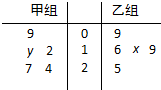如图茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩（单位：分），已知甲组数据的中位数为17，乙组数据的平均数为17.4，则x，y的值分别为（ ）| A、7，8 | B、5，7 |
| C、8，5 | D、8，7 |
函数f（x）=xlnx在x=1处的切线为（ ）
| A、y=x+1 |
| B、y=x-1 |
| C、y=1-x |
| D、y=1-2x |
在极坐标系中，点（
，
）到直线ρcosθ-ρsinθ-1=0的距离等于（ ）
| 2 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
O为坐标原点，F为抛物线C：y2=4x的焦点，P为C上一点，若|PF|=3．则△POF的面积为（ ）
A、
| ||
B、2
| ||
C、
| ||
D、2
|
在等差数列{an}中，a1+a2+a3=3，a28+a29+a30=165，则此数列前30项和等于（ ）
| A、810 | B、840 |
| C、870 | D、900 |