题目内容
过点P（3，4）的动直线与两坐标轴的交点分别为A，B，过A，B分别作两轴的垂线交于点M，求点M的轨迹方程．
考点：轨迹方程
专题：计算题,直线与圆
分析：出M坐标，求出A，B坐标，利用
，
共线，求出x，y的关系式，就是所求M的轨迹方程．
| AP |
| PB |
解答：
解：设M（x，y）由题意可知A（x，0），B（0，y），
因为A，B，P三点共线，所以
，
共线，
因为
=（3-x，4），
=（-3，y-4），
所以（3-x）（y-4）=-12，即4x+3y=xy，
所以点M的轨迹方程为：4x+3y=xy．
因为A，B，P三点共线，所以
| AP |
| PB |
因为
| AP |
| PB |
所以（3-x）（y-4）=-12，即4x+3y=xy，
所以点M的轨迹方程为：4x+3y=xy．
点评：本题考查曲线轨迹方程的求法，考查转化思想计算能力．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
若X～N（μ，σ2），P（μ-σ＜X≤μ+σ）=0.7，则P（X≤μ-σ）=（ ）
| A、0.15 | B、0.3 |
| C、0.35 | D、0.65 |
从装有两个红球和两个黑球的口袋内任取两个球，那么互斥而不对立的两个事件是（ ）
| A、“至少有一个黑球”与“都是黑球” |
| B、“恰有一个黑球”与“恰有两个黑球” |
| C、“至少有一个黑球”与“至少有一个红球” |
| D、“至少有一个黑球”与“都是红球” |
如图，AB是⊙O的直径，P在AB的延长线上，PC切⊙O于C，PC=
，BP=1，则⊙O的半径为（ ）
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
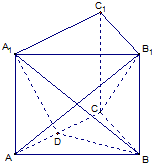如图所示，正三棱柱ABC-A1B1C1的底面边长是2，侧棱长是