在正项等比数列{an}中.log2a3+log2a6+log2a9=3.则a1•a11的值是．题目和参考答案——青夏教育精英家教网—

题目内容

在正项等比数列{a_n}中，log₂a₃+log₂a₆+log₂a₉=3，则a₁•a₁₁的值是

．

考点：等比数列的性质,对数的运算性质

专题：等差数列与等比数列

分析：由对数的运算和等比数列的性质可得a₆=2，进而可得a₁•a₁₁=a₆²=4．

解答： 解：∵在正项等比数列{a_n}中，log₂a₃+log₂a₆+log₂a₉=3，
∴log₂a₃•a₆•a₉=3，∴log₂a₆³=3，解得a₆=2，
∴a₁•a₁₁=a₆²=4
故答案为：4

点评：本题考查等比数列的性质，涉及对数的运算，属中档题．

练习册系列答案

名师导航小学毕业升学总复习系列答案

黄冈口算题卡系列答案

一通百通小学毕业升学模拟测试卷系列答案

典元教辅小学毕业升学必备小升初押题卷系列答案

相关题目

设复数z满足z•（1-i）=2，则复数z的模|z|等于（　　）

，g（x）=lnx．
（1）求函数f（x）在点（1，0）处的切线y=h（x）；
（2）在（1）的条件下，证明：对任意的x∈（0，+∞），h（x）-g（x）≥

f（x）恒成立；
（3）若对于任意的x₁＞x₂＞0，f（x₁）-f（x₂）＞m[g（x₁）-g（x₂）]都成立，求实数m的取值范围．

已知椭圆C的中心在坐标原点，右焦点为F(

，0)，A、B是椭圆C的左、右顶点，D是椭圆C上异于A、B的动点，且△ADB面积的最大值为12．
（1）求椭圆C的方程；
（2）求证：当点P（x₀，y₀）在椭圆C上运动时，直线l：x₀x+y₀y=2与圆O：x²+y²=1恒有两个交点，并求直线l被圆O所截得的弦长L的取值范围．

求方程[x³]+[x²]+[x]={x}-1的解．

在平面直角坐标系xOy中，P是直线2x+2y-1=0上的一点，Q是射线OP上的一点，满足|OP|•|OQ|=1．
（Ⅰ）求Q点的轨迹；
（Ⅱ）设点M（x，y）是（Ⅰ）中轨迹上任意一点，求x+7y的最大值．

若△ABC的外接圆是半径为1的圆O，且∠AOB=120°，则

•

的取值范围为

．

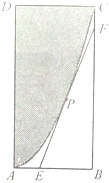如图，有一个长方形地块ABCD，边AB为2km，AD为4km．，地块的一角是湿地（图中阴影部分），其边缘线AC是以直线AD为对称轴，以A为顶点的抛物线的一部分．现要铺设一条过边缘线AC上一点P的直线型隔离带EF，E，F分别在边AB，BC上（隔离带不能穿越湿地，且占地面积忽略不计）．设点P到边AD的距离为t（单位：km），△BEF的面积为S（单位：km²）．
（1）求S关于t的函数解析式，并指出该函数的定义域；
（2）是否存在点P，使隔离出的△BEF面积S超过3km²？并说明理由．

已知函数f（x）=sin（2x+φ），其中φ∈（0，2π），若f（x）≤|f（

）|对x∈R恒成立，且f（

）＜f（π），则f（x）的单调递增区间是（　　）

试题分类