题目内容
 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆的方程;
(2)设A、B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,若|AF1|-|BF2|=
| ||
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)根据椭圆的性质和已知(1,e)和(e,
),都在椭圆上列式求解.
(2)设AF1与BF2的方程分别为x+1=my,x-1=my,与椭圆方程联立,求出|AF1|、|BF2|,根据已知条件AF1-BF2=
,用待定系数法求解
| ||
| 2 |
(2)设AF1与BF2的方程分别为x+1=my,x-1=my,与椭圆方程联立,求出|AF1|、|BF2|,根据已知条件AF1-BF2=
| ||
| 2 |
解答:
解:(1)∵椭圆
+
=1(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0),
点(1,e)和(e,
)都在椭圆上,
∴
,
∵e2=
=
=1-
,
∴
+
=
+
=
+
-
=1,解得b2=1,
∵
+
=
+
=1,
∴a4-4a2+4=(a2-2)=0,解得a2=2,
∴椭圆方程为
+y2=1.
(2)∵椭圆方程为
+y2=1,∴F1(-1,0),F2(1,0),
又∵直线AF1与直线BF2平行,∴设AF1与BF2的方程分别为x+1=my,x-1=my.
设A(x1,y1),B(x2,y2),y1>0,y2>0,
∴由
,得(m2+2)y12-2my1-1=0.
∴y1 =
,或y1=
(舍),
∴|AF1|=
×|0-y1|=
,①
同理|BF2|=
,②
∵|AF1|-|BF2|=
,
∴由①②得|AF1|-|BF2|=
=
,解得m2=2.
∵注意到m>0,∴m=
.
∴直线AF1的斜率为
=
.
| x2 |
| a2 |
| y2 |
| b2 |
点(1,e)和(e,
| ||
| 2 |
∴
|
∵e2=
| c2 |
| a2 |
| a2-b2 |
| a2 |
| b2 |
| a2 |
∴
| 1 |
| a2 |
| e2 |
| b2 |
| 1 |
| a2 |
1-
| ||
| b2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| a2 |
∵
| e2 |
| a2 |
| 3 |
| 4b2 |
| a2-b2 |
| a4 |
| 3 |
| 4b2 |
∴a4-4a2+4=(a2-2)=0,解得a2=2,
∴椭圆方程为
| x2 |
| 2 |
(2)∵椭圆方程为
| x2 |
| 2 |
又∵直线AF1与直线BF2平行,∴设AF1与BF2的方程分别为x+1=my,x-1=my.
设A(x1,y1),B(x2,y2),y1>0,y2>0,
∴由
|
∴y1 =
m+
| ||
| m2+2 |
m-
| ||
| m2+2 |
∴|AF1|=
| m2+1 |
| ||||
| m2+2 |
同理|BF2|=
| ||||
| m2+2 |
∵|AF1|-|BF2|=
| ||
| 2 |
∴由①②得|AF1|-|BF2|=
2m
| ||
| m2+2 |
| ||
| 2 |
∵注意到m>0,∴m=
| 2 |
∴直线AF1的斜率为
| 1 |
| m |
| ||
| 2 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生的计算能力,解题时要注意等价转化思想的合理运用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
双曲线
-
=1的离心率e=2,则双曲线的渐近线方程为( )
| y2 |
| 16 |
| x2 |
| m |
A、y=±
| ||||
B、y=±
| ||||
| C、y=±2x | ||||
D、y=±
|
 为监测幼儿身体发育状况,某幼儿园对“大班”的100名幼儿的体重做了测量,并根据所得数据画出了频率分布直方图,如图所示.则体重在[18,20](单位kg)的幼儿人数为( )
为监测幼儿身体发育状况,某幼儿园对“大班”的100名幼儿的体重做了测量,并根据所得数据画出了频率分布直方图,如图所示.则体重在[18,20](单位kg)的幼儿人数为( )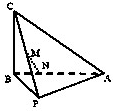 如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.
如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB. 如图,直线PA为圆O的切线,切点为A,直径BC⊥OP,连接AB交PO于点D.
如图,直线PA为圆O的切线,切点为A,直径BC⊥OP,连接AB交PO于点D.