题目内容
5.某学生对函数f( x )=x•cosx的性质进行研究,得出如下的结论:①函数y=f(x)在[-π,0]上单调递增,在[0,π]上单调递减;
②点($\frac{π}{2}$,0)是函数y=f(x)图象的一个对称中心;
③函数y=f(x)图象关于直线x=π对称;
④存在常数M>0,使|f(x)|≤M|x|对一切实数x 均成立.其中正确命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用特值法判断前3个结论,再判断第4个结论即可.
解答 解:①特值法.f(-π)=π,f(0)=0,故函数y=f(x)在[-π,0]上单调递增错,
②若关于($\frac{π}{2}$,0)中心对称,则f(x)=-f(π-x),而f(π)=-π,f(0)=0,故②错.
③若函数y=f(x)图象关于直线x=π对称,则f(x)=f(2π-x),
而f(2π)=2π,f(0)=0,故③错.
④当x=0时,|f(0)|≤M•0,
当x≠0时,M≥|$\frac{f(x)}{x}$|=|cosx|恒成立,
故M≥1即可,所以④正确.
故选:A.
点评 本题考查了函数的性质的判断与应用.

练习册系列答案
相关题目
15.已知a∈R,不等式$\frac{x-3}{x+a}>1$的解集为P,且-4∉P,则a的取值范围是( )
| A. | a≥-4 | B. | -3<a≤4 | C. | a≥4或a≤-3 | D. | a≥4或a<-3 |
16.两条平行线3x+4y-12=0与ax+8y-4=0之间的距离为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.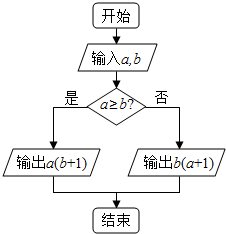 对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )
对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )
 对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )
对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )| A. | 8 | B. | 15 | C. | 16 | D. | $\frac{3}{2}$ |
10. 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<ω)的图象如图所示,为了得到g(x)=Asinωx的图象,可以将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<ω)的图象如图所示,为了得到g(x)=Asinωx的图象,可以将f(x)的图象( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<ω)的图象如图所示,为了得到g(x)=Asinωx的图象,可以将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<ω)的图象如图所示,为了得到g(x)=Asinωx的图象,可以将f(x)的图象( )| A. | 向右平移$\frac{π}{12}$个单位长度 | B. | 向左平移$\frac{π}{12}$个单位长度 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
14.函数f(x)=tanωx(ω>0)的图象的相邻两支截直线$y=\frac{π}{8}$所得线段长为$\frac{π}{8}$,则$f(\frac{π}{8})$的值是( )
| A. | 0 | B. | -1 | C. | 1 | D. | $\frac{π}{8}$ |