题目内容
如图所示,直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,求k的值.
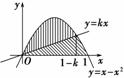
解析 抛物线y=x-x2与x轴两交点的横坐标为x1=0,x2=1,
所以,抛物线与x轴所围图形的面积
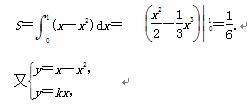 由此可得,
由此可得,
抛物线y=x-x2与y=kx两交点的横坐标为
x3=0,x4=1-k,所以,
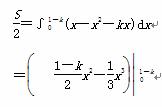 =
=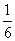 (1-k)3.
(1-k)3.
又知S=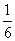 ,
,
所以(1-k)3=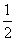 ,
,
于是k=1- 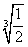 =1-
=1-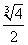 .
.

练习册系列答案
相关题目
题目内容
如图所示,直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,求k的值.

解析 抛物线y=x-x2与x轴两交点的横坐标为x1=0,x2=1,
所以,抛物线与x轴所围图形的面积
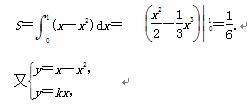 由此可得,
由此可得,
抛物线y=x-x2与y=kx两交点的横坐标为
x3=0,x4=1-k,所以,
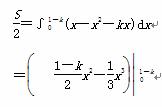 =
=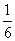 (1-k)3.
(1-k)3.
又知S=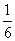 ,
,
所以(1-k)3=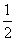 ,
,
于是k=1- 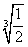 =1-
=1-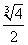 .
.
