题目内容
2.使不等式tanx$≥\sqrt{3}$成立的x的集合为( )| A. | (kπ+$\frac{π}{6}$,kπ+$\frac{π}{2}$)k∈Z | B. | [kπ+$\frac{π}{6}$,kπ+$\frac{π}{2}$)k∈Z | C. | [kπ+$\frac{π}{3}$,kπ+$\frac{π}{2}$)k∈Z | D. | (kπ+$\frac{π}{3}$,kπ+$\frac{π}{2}$)k∈Z |
分析 根据正切函数的图象和性质,即可求出不等式的解集.
解答 解:∵不等式tanx$≥\sqrt{3}$,
由正切函数的性质可得
kπ+$\frac{π}{3}$≤x<kπ+$\frac{π}{2}$,
∴使不等式成立的x的集合为{x|kπ+$\frac{π}{3}$≤x<kπ+$\frac{π}{2}$,k∈Z};
即[kπ+$\frac{π}{3}$,kπ+$\frac{π}{2}$).
故选:C.
点评 本题考查了利用正切函数的图象和性质解不等式的应用问题,是基础题目.

练习册系列答案
相关题目
17.已知函数f(x)=|2x-1|,g(x)=x2-(2+3k)x+2k+1,若函数y=g[f(x)]有3个不同零点,则k的范围是( )
| A. | k=-$\frac{1}{2}$或k>0 | B. | -$\frac{1}{2}$<k<0或k>0 | C. | k≥-$\frac{1}{2}$ | D. | k≥0 |
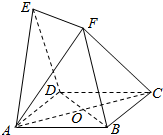 如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.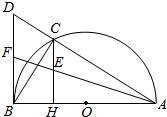 如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,
如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,