Question

（1）在区间（0，1）内任选一个数a，求能使方程x²+2ax+

1

2

=0有两个不相等的实根的概率；
（2）某校规定周末18：30开始考勤，假设该校学生小张与小王在18：00-18：25之间到校，且每人在该时间段的任何时刻到校是等可能的，求小张与小王到校时间相差5分钟之内的概率．

Answer 1

考点：几何概型

专题：概率与统计

分析：（1）要使方程x²+2ax+

1

2

=0有两个不相等的实根，则有△=（2a）²-4×

1

2

=4a²-2＞0，由此能求出能使方程x²+2ax+

1

2

=0有两个不相等的实根的概率．
（2）设18：00为0时刻，小张、小王到校的时刻分别为x，y，则

0≤x≤25 0≤y≤25 |x-y|≤5

，由此能求出小张与小王到校时间相差5分钟之内的概率．

解答： 解：（1）要使方程x²+2ax+

1

2

=0有两个不相等的实根，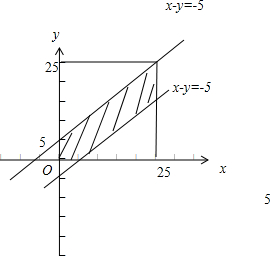
则有△=（2a）²-4×

1

2

=4a²-2＞0，
必须有a²＞

1

2

，
所以a＞

2

2

，由几何概率的定义知所求概率：
p=

1- 2 2

1

=1-

2

2

．
（2）设18：00为0时刻，小张、小王到校的时刻分别为x，y，
则

0≤x≤25 0≤y≤25 |x-y|≤5

，
作出可行域如图，
∴小张与小王到校时间相差5分钟之内的概率：
p=1-

20×25+20×20

25×25

×

1

2

=

7

25

．

点评：本题考查概率的求法，是中档题，解题时要认真审题，注意根的判别式和线性规划的合理运用．