题目内容
7.已知等差数列{an}的前n项和为Sn,且a4=8,a6=12.(1)求数列{an}的通项公式;
(2)若Sn=20,求n的值.
分析 (1)利用等差数列的通项公式列出方程组,求出首项和公差,由此能求出数列{an}的通项公式.
(2)利用等差数列通项公式及Sn=20,能求出n的值.
解答 解:(1)∵等差数列{an}的前n项和为Sn,且a4=8,a6=12.
∴$\left\{\begin{array}{l}{{a}_{4}={a}_{1}+3d=8}\\{{a}_{6}={a}_{1}+5d=12}\end{array}\right.$,
解得a1=2,d=2,
∴数列{an}的通项公式an=a1+(n-1)d=2+(n-1)×2=2n.
(2)∵Sn=20,
∴${S}_{n}=\frac{n}{2}({a}_{1}+{a}_{n})$=$\frac{n}{2}(2+2n)$=n2+n=20,
解得n=4或n=-5,∵n∈N*,
∴n的值为4.
点评 本题考查等差数列的通项公式及项数的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
15.已知函数$f(x)=\left\{{\begin{array}{l}{{{log}_2}x,x>0}\\{\frac{1}{3^x},x≤0}\end{array}}\right.$,则$f(f(\frac{1}{4}))$=( )
| A. | 9 | B. | $\frac{1}{9}$ | C. | $\frac{2}{9}$ | D. | $-\frac{2}{3}$ |
2.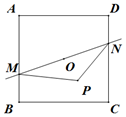 正方形ABCD边长为2,中心为O,直线l经过中心O,交AB于M,交CD于N,P为平面上一点,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )
正方形ABCD边长为2,中心为O,直线l经过中心O,交AB于M,交CD于N,P为平面上一点,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )
 正方形ABCD边长为2,中心为O,直线l经过中心O,交AB于M,交CD于N,P为平面上一点,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )
正方形ABCD边长为2,中心为O,直线l经过中心O,交AB于M,交CD于N,P为平面上一点,且$2\overrightarrow{OP}=λ\overrightarrow{OB}+(1-λ)\overrightarrow{OC}$,则$\overrightarrow{PM}•\overrightarrow{PN}$的最小值是( )| A. | $-\frac{3}{4}$ | B. | -1 | C. | $-\frac{7}{4}$ | D. | -2 |
19.在△ABC中,内角A,B,C的对边分别是a,b,c,则a2-b2=$\sqrt{3}$bc,sinC=$\sqrt{3}$sinB则C=( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
17.现有10个数,它们能构成一个以2为首项,-2为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |