题目内容
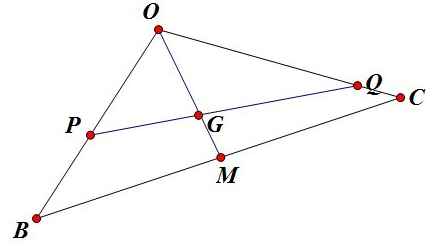
如图，G为△OBC的重心，PQ为过重心的直线，交OB与OC于P，Q点．
①用
，
表示
；
②若
=x
，
=y
，求证
+
为定值．
①用
| OP |
| OQ |
| OG |
②若
| OP |
| OA |
| OQ |
| OB |
| 1 |
| x |
| 1 |
| y |
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：①由于点P、G、Q三点共线，利用向量共线定理可得：存在实数λ使得
=λ
．化简即可得出．
②利用①的结论和重心定理、向量的平行四边形法则即可得出．
| PG |
| GQ |
②利用①的结论和重心定理、向量的平行四边形法则即可得出．
解答：
①解：∵点P、G、Q三点共线，∴存在实数λ使得
=λ
．
∴
-
=λ(
-OG)，
化为
=
+
.(λ∈[
，2])．
②证明：∵
=x
，
=y
，
∴
=
+
，
又
=
=
×
(
+
)=
+
，
∴
=
，
=
．
∴
+
=
+
=3为定值．
| PG |
| GQ |
∴
| OG |
| OP |
| OQ |
化为
| OG |
| 1 |
| 1+λ |
| OP |
| λ |
| 1+λ |
| OQ |
| 1 |
| 2 |
②证明：∵
| OP |
| OA |
| OQ |
| OB |
∴
| OG |
| x |
| 1+λ |
| OA |
| λy |
| 1+λ |
| OB |
又
| OG |
| 2 |
| 3 |
| OM |
| 2 |
| 3 |
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
∴
| x |
| 1+λ |
| 1 |
| 3 |
| λy |
| 1+λ |
| 1 |
| 3 |
∴
| 1 |
| x |
| 1 |
| y |
| 3 |
| 1+λ |
| 3λ |
| 1+λ |
点评：本题考查了向量共线定理、重心定理、向量的平行四边形法则等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
对任意的实数m，直线y=mx+1与圆x2+y2=4的位置关系一定是（ ）
| A、相切 |
| B、相交且直线过圆心 |
| C、相交且直线不过圆心 |
| D、相离 |