题目内容
直线l：3x+4y-25=0与圆C：x2+y2-6x-8y=0的位置关系是（ ）
| A、相离 | B、相切 |
| C、相交且过圆心 | D、相交但不过圆心 |
考点：直线与圆的位置关系
专题：直线与圆
分析：把圆的方程化为标准方程后，找出圆心坐标与圆的半径r，然后利用点到直线的距离公式求出圆心到已知直线的距离d，然后比较d与r的大小即可得到直线与圆的位置关系，然后把圆心坐标代入已知直线即可判断已知直线是否过圆心．
解答：
解：由圆的方程x2+y2-6x-8y=0化为标准方程得：（x-3）2+（y-4）2=25，
所以圆心坐标为（3，4），圆的半径r=5，
显然圆的圆心满足直线3x+4y-25=0，
所以直线与圆相交并且经过圆心．
故选：C．
所以圆心坐标为（3，4），圆的半径r=5，
显然圆的圆心满足直线3x+4y-25=0，
所以直线与圆相交并且经过圆心．
故选：C．
点评：此题考查学生掌握判断直线与圆位置关系的方法，灵活运用点到直线的距离公式化简求值，是一道综合题．
练习册系列答案
阅读快车系列答案
相关题目
x2=49的充分必要条件是（ ）
| A、x=7 |
| B、x=-7 |
| C、x=7或x=-7 |
| D、x=7且x=-7 |
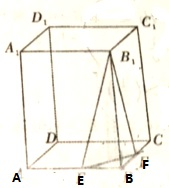已知正四棱柱ABCD-A1B1C1D1，其底面边长为4，高为
如图，平面直角坐标系中，动点P（x，y），PM⊥y轴，垂足为M，点N与点P关于x轴对称，且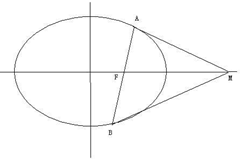
如图，椭圆在下列函数中，最小值为2的是（ ）
A、y=
| ||||||
B、y=lgx+
| ||||||
C、y=x+
| ||||||
| D、y=x2-2x+4 |