题目内容
(1+x+x2)(x2-
)6的展开式中的常数项为 .
| 1 |
| x |
考点:二项式系数的性质
专题:二项式定理
分析:根据题意,写出(x2-
)6的展开式中的通项为Tr+1,令x的指数为0,-1,-2可得r的值,由项数与r的关系,可得答案.
| 1 |
| x |
解答:
解:(x2-
)6的展开式中的通项为Tr+1 =
•(-1)r•x12-3r,
令12-3r=0,求得r=4,12-3r=-1,求得r无解,12-3r=-2,求得r无解,
故(1+x+x2)(x2-
)6的展开式中的常数项为
=15,
故答案为:15.
| 1 |
| x |
| C | r 6 |
令12-3r=0,求得r=4,12-3r=-1,求得r无解,12-3r=-2,求得r无解,
故(1+x+x2)(x2-
| 1 |
| x |
| C | 4 6 |
故答案为:15.
点评:本题考查等价转化的能力、考查利用二项展开式的通项公式解决二项展开式的特殊项问题,属于中档题.

练习册系列答案
相关题目
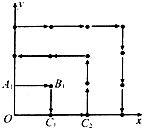 某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点Al(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么:
某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点Al(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么: