题目内容
16．已知sinα-cosα=-$\frac{5}{4}$，且-$\frac{π}{4}$＜α＜0．求：（1）sinαcosα的值；
（2）cosα的值．
分析 （1）已知式子平方结合二倍角公式可得；
（2）由题意和完全平方式的特点可得sinα+cosα的值，解方程组可得．
解答 解：（1）∵sinα-cosα=-$\frac{5}{4}$，且-$\frac{π}{4}$＜α＜0，
∴（sinα-cosα）2=$\frac{25}{16}$，∴1-2sinαcosα=$\frac{25}{16}$，
∴sinαcosα=-$\frac{9}{32}$；
（2）∵（sinα+cosα）2=（sinα-cosα）2+4sinαcosα=$\frac{7}{16}$，
又∵-$\frac{π}{4}$＜α＜0，∴sinα+cosα＞0，∴sinα+cosα=$\frac{\sqrt{7}}{4}$，
联立sinα-cosα=-$\frac{5}{4}$和sinα+cosα=$\frac{\sqrt{7}}{4}$可解得cosα=$\frac{5+\sqrt{7}}{8}$
点评 本题考查三角函数公式和方程的解法，属基础题．
练习册系列答案
相关题目
4．一物体的运动方程是s=$\frac{1}{2}$at2（a为常数），则该物体在t=t0时的瞬时速度是（ ）
| A． | at0 | B． | -at0 | C． | $\frac{1}{2}$at0 | D． | 2at0 |
1．有8人已站成一排，现在要求其中4人位置不变，其余4人调换位置，则有（ ）种不同的调换方法．
| A． | 1680 | B． | 256 | C． | 630 | D． | 280 |
8．已知点P（t，$\sqrt{3}$）为锐角φ终边上的一点，且cosφ=$\frac{t}{2}$，若函数f（x）=2sin（ωx+φ）（ω＞0）的图象与直线y=2相邻的两交点之间的距离为π，则函数f（x）的一条对称轴为（ ）
| A． | x=$\frac{π}{12}$ | B． | x=$\frac{π}{6}$ | C． | x=$\frac{π}{3}$ | D． | x=$\frac{π}{2}$ |
某产品的广告费用x与销售额y的统计数据如下表：
广告费用x（万元） | 4 | 2 | 3 | 5 |
销售额y（万元） | 49 | 26 | 39 | 54 |
根据上表可得回归方程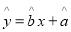
中的
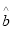为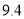
，据此模型预报广告费用为6万元时销售额为 （ ）
A. 63．6万元 B. 65．5万元 C. 67．7万元 D. 72．0万元