题目内容
10.设a>1,x,y满足约束条件$\left\{\begin{array}{l}{y≥x}\\{y≤ax}\\{x+2y≤2}\end{array}\right.$,若目标函数z=x+ay最大值不小于$\frac{3}{2}$,则实数a的取值范围为( )| A. | a≥0 | B. | a≥$\frac{3}{2}$ | C. | a≥$\frac{3+\sqrt{5}}{4}$ | D. | a≥$\frac{5}{4}$ |
分析 画出满足条件的平面区域,求出角点的坐标,由z=x+ay得:y=-$\frac{1}{a}$x+$\frac{z}{a}$,通过讨论a的范围,得到关于a的不等式,求出a的范围即可.
解答 解:画出满足条件的平面区域,如图示: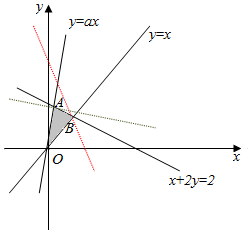 ,
,
由$\left\{\begin{array}{l}{y=ax}\\{x+2y=2}\end{array}\right.$,解得:A($\frac{2}{1+2a}$,$\frac{2a}{1+2a}$),
由$\left\{\begin{array}{l}{y=x}\\{x+2y=2}\end{array}\right.$,解得:B($\frac{2}{3}$,$\frac{2}{3}$),
由z=x+ay得:y=-$\frac{1}{a}$x+$\frac{z}{a}$,
a>2时,-$\frac{1}{2}$<-$\frac{1}{a}$<0,
直线过A($\frac{2}{1+2a}$,$\frac{2a}{1+2a}$)时,z最大,(图中绿线),
此时,z=$\frac{2+{2a}^{2}}{1+2a}$≥$\frac{3}{2}$,解得:a≥$\frac{3+\sqrt{5}}{4}$或a≤$\frac{3-\sqrt{5}}{4}$,
1<a<2时,-1<-$\frac{1}{a}$<-$\frac{1}{2}$,
直线过B($\frac{2}{3}$,$\frac{2}{3}$)时,z最大(图中红线),
此时,z=$\frac{2+2a}{3}$≥$\frac{3}{2}$,解得:a≥$\frac{5}{4}$,
a=2时,直线y=-$\frac{1}{2}$x+$\frac{z}{2}$和直线y=-$\frac{1}{2}$x+1重合时,z最大,
此时z=2>$\frac{3}{2}$,符合题意,
综上,a≥$\frac{5}{4}$,
故选:D.
点评 本题考查了简单的线性规划问题,考查数形结合思想,讨论a的范围确定直线过A还是B是解题的关键,本题是一道中档题.

